Una aplicación Imaginaria para mi Tranquilidad| + Ficha Técnica |
| + Mapa Publicaciones |
| + Videos Asociados |
|
Eliminar una Singularidad Disruptiva  Armonía Imaginemos un entorno natural tranquilo, donde se percibe un sonido suave y casi continuo del viento, acompañado por el trinar regular de los pájaros. Este paisaje sonoro transmite una sensación de armonía, continuidad y estabilidad temporal.1 Sin embargo, de manera ocasional y abrupta, irrumpe en las cercanías el ruido de un motor u otro artefacto mecánico. Esta aparición repentina introduce una interrupción clara y localizada del equilibrio acústico previo, rompiendo la continuidad percibida del entorno2.  Irrupción Ante esta experiencia surge una pregunta natural:
En otras palabras, ¿sería posible disponer de una aplicación —análoga a una inmersión diferenciable en dispositivo móvil?, dotada de un software personal con audífono, asistido por inteligencia artificial — que integre el ruido disruptivo dentro de un paisaje sonoro más amplio, eliminando su carácter intrusivo sin destruir la estructura global del sonido. Situaciones como leer el periódico en casa o descansar en silencio, interrumpidas de pronto por el ruido persistente de una cortadora de césped en la vecindad, ilustran claramente este problema cotidiano3. |
||
|
Dispositivos Reales y Límites Físicos  Dispositivos Actuales (ANC) Desde el punto de vista físico, se sabe que existen sistemas y aplicaciones acústicas capaces de atenuar o suprimir el ruido proveniente de fuentes específicas —como motores, ventiladores o cortadoras de césped— mientras se preservan o permiten el paso de sonidos suaves y armónicos del entorno. El objetivo central de estos sistemas no es la eliminación indiscriminada del sonido, sino la aplicación de una transformación acústica selectiva, fundamentada en modelos físicos y matemáticos que describen la propagación, interferencia y superposición de ondas sonoras. Sin embargo, los sistemas actuales de Active Noise Cancellation (ANC) presentan limitaciones físicas inevitables. Su desempeño es significativamente mejor frente a ruidos periódicos o cuasi-periódicos, de espectro estable y provenientes de direcciones conocidas. En contraste, resultan menos eficaces ante ruidos caóticos, impulsivos o impredecibles, como golpes aleatorios, gritos o sonidos repentinos. A pesar de estas restricciones, los sistemas ANC pueden interpretarse conceptualmente como transformaciones espectrales y espaciales de la señal acústica, y continúan siendo objeto de investigación activa y desarrollo de prototipos experimentales orientados a mejorar su adaptabilidad y precisión. En la actualidad, existen numerosos audífonos inalámbricos que incorporan tecnología de Control Activo de Ruido. Estos dispositivos están diseñados para reducir de manera significativa ruidos externos como motores, tráfico urbano o zumbidos constantes. Su funcionamiento se basa en micrófonos que captan el sonido ambiental y generan una onda acústica opuesta que cancela parcialmente el ruido detectado. No obstante, su efectividad es mayor en bajas frecuencias, suelen implicar un alto consumo energético, presentan costos elevados y, en muchos casos, están pensados para usos breves o situaciones puntuales, como conversaciones rápidas o desplazamientos cortos. Intento Ficticio: Una Inmersión Matemática Desde una interpretación geométrica idealizada, el objetivo no sería colapsar ni eliminar información local, sino preservar la estructura fina de la señal y desplegarla en un espacio de mayor dimensión, donde el ruido y la señal armónica puedan coexistir en direcciones distintas. Siguiendo el artículo base Concepto de Inmersión ~ Geometría Diferencial"  , se modela el paisaje sonoro como una señal suave en el tiempo:
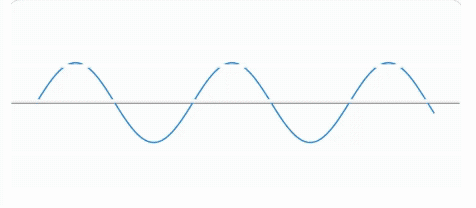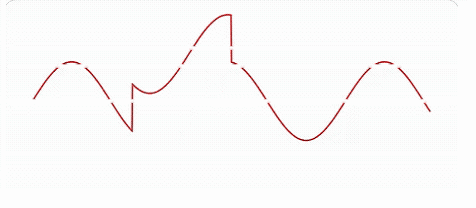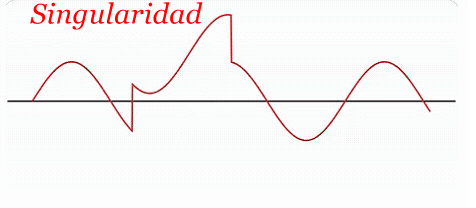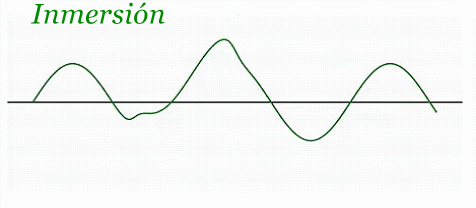
El ruido del motor se modela como una perturbación localizada: $$ r(t) = A,\chi_{[t_1,t_2]}(t), $$ donde \(A\) representa la amplitud del ruido y \([t_1,t_2]\) el intervalo temporal durante el cual el motor es audible. El sonido percibido es entonces: $$ s(t) = s_0(t) + r(t). $$ Este modelo describe un ruido constante pero abrupto, que aparece y desaparece súbitamente, introduciendo discontinuidades en \(t_1\) y \(t_2\). Fuera del intervalo \([t_1,t_2]\), la señal es suave; dentro de él, la señal se desplaza bruscamente por una constante, generando quiebres perceptivos que el oído humano identifica como intrusivos o artificiales.5 Esta aplicación podría implementarse en el propio teléfono móvil y utilizarse con audífonos, capaz de filtrar sonidos disruptivos mediante inmersiones diferenciales, previamente detectados y supervisados por el propio usuario. Idea de Inmersión Acústica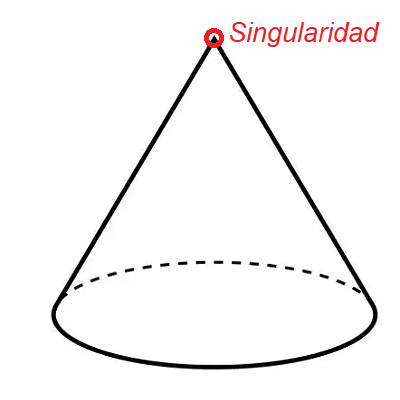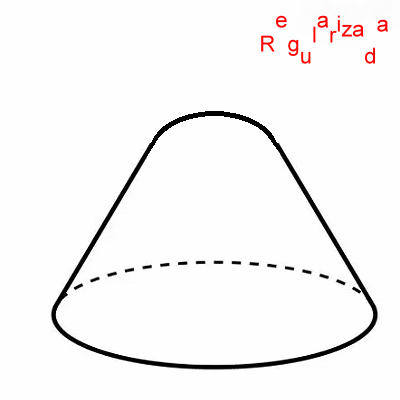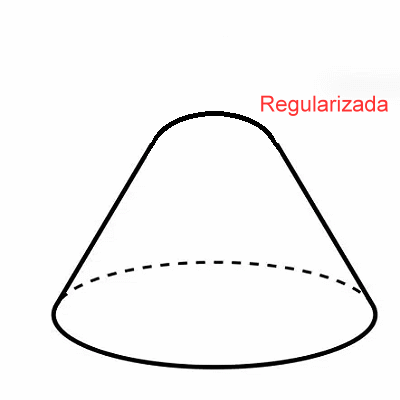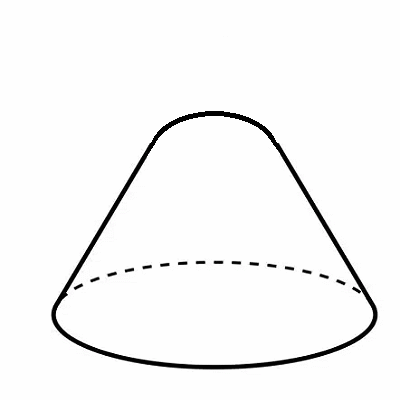 
Para "eliminar" esta singularidad acústica sin destruir la señal original, se propone conceptualmente una transformación geométrica:
En un espacio de mayor dimensión, la señal puede representarse como una curva diferenciable, incluso en presencia de cambios bruscos. Formalmente, se construye una aplicación $$ \mathit{\Phi} : \mathbb{R} \to \mathbb{R}^n $$ tal que \( \mathit{\Phi} \) es una inmersión diferenciable. En este nuevo espacio, la singularidad no desaparece, sino que se redistribuye geométricamente, preservando la estructura local de la señal. Este es el principio geométrico fundamental: no eliminar la perturbación, sino cambiar el espacio donde vive6. Explicación Conceptual y Matemática Sea una señal acústica temporal \( s(t) \), compuesta por:
\(r(t) \): ruido disruptivo, no armónico y de comportamiento irregular. El objetivo no es restar directamente \( r(t) \), sino construir una transformación geométrica $$ \mathit{\Phi} : X \to Y $$ donde:
\(Y\) es una variedad diferenciable donde las componentes se separan geométricamente. La transformación \( \mathit{\Phi} \) es una inmersión diferenciable, ya que preserva información local, mantiene vectores tangentes no degenerados y permite analizar la señal desde una perspectiva geométrica más rica.  Usando Aplicación Ficticia Armónica Síntesis Matemática En síntesis conceptualmente se partió de una señal armónica suave \(s_0(t)\in C^\infty(\mathbb{R})\) con un ruido no suave $$ r(t)=A,\chi_{[t_1,t_2]}(t) $$ Este ruido se regularizó con: $$ r_\varepsilon(t)=A\Big(\sigma\big(\tfrac{t-t_1}{\varepsilon}\big)-\sigma\big(\tfrac{t-t_2}{\varepsilon}\big)\Big) $$ $$ \text{con}\quad\varepsilon \longrightarrow 0 $$ Donde \(\sigma:\mathbb{R}\to(0,1)\) una función sigmoide suave, de la forma exponencial estándar: $$ \sigma(x)=\frac{1}{1+e^{-x}} $$ Se definió la inmersión: $$ \mathit{\Phi}(t)=\big(s_0(t),r_\varepsilon(t)\big) $$ \(\implies\)
En \(\mathbb{R}^2\): hay curva suave El ruido deja de ser singular y pasa a ser dirección transversal Esta sería una inmersión diferenciable que cumple con la solución ficticia imaginada. |
