| + Ficha Técnica |
| + Mapa Publicaciones |
| + Videos Asociados |
Video Asociado|
Introducción El objetivo de esta presentación es mostrar cómo una superficie suave y diferenciable puede definirse a partir de un conjunto simple de ecuaciones diferenciales ordinarias, explicando su significado geométrico y las razones por las cuales estas ecuaciones garantizan suavidad. Se adopta el enfoque estándar de la geometría diferencial, utilizando dos tipos de EDO: ecuaciones diferenciales simples y ecuaciones diferenciales parametrizadas. Ambas describen curvas suaves, las cuales pueden interpretarse como subvariedades unidimensionales del plano \(\mathbb{R}^2\) o, mediante la introducción de parámetros adicionales, como superficies parametrizadas en espacios de mayor dimensión1. Definición de una superficie mediante EDOs Una curva suave \(C\) en el plano puede definirse como la solución de una ecuación diferencial ordinaria de primer orden. Por ejemplo, $$ \frac{dy}{dx} = f(x) $$ Consideremos el caso particular: $$ \frac{dy}{dx} = 2x \quad \implies \quad dy = 2x dx $$ Integrando respecto de \(x\): $$ y(x) = \int 2x \, dx = x^2 + C $$ Se obtiene así una familia de soluciones, donde cada valor de la constante \(C \in \mathbb{R}\) define una curva distinta. Este conjunto de curvas puede interpretarse como una foliación del plano \(\mathbb{R}^2\).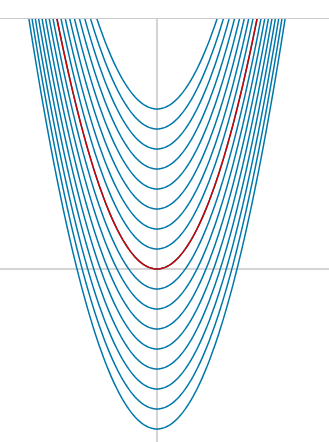 
Plano foliado por parábolas2
De este modo, el plano queda foliado3 por parábolas que no se intersectan, generando una estructura suave. Esto ilustra cómo una curva suave puede definirse naturalmente como solución de una ecuación diferencial ordinaria. Ahora se construye una superficie suave en \(\mathbb{R}^3\) a partir de un sistema de ecuaciones diferenciales ordinarias parametrizadas. Estas ecuaciones definen una familia de curvas integrales que, al variar un parámetro adicional, generan una superficie completa. Sean \(s\) el parámetro de la curva y \(t\) el parámetro que indexa la familia de curvas. Se considera el sistema: $$ \begin{cases} \frac{dx}{ds} = \cos t \\ \frac{dy}{ds} = \sin t \\ \frac{dz}{ds} = s \end{cases} $$ con condiciones iniciales: $$ x(0,t)=0,\quad y(0,t)=0,\quad z(0,t)=0 $$ Integrando con respecto a \(s\), se obtiene4: $$ \require{cancel} \begin{cases} dx = \int \ \cos t \ ds = s\cos t + \cancelto{0}{C_1}\\ dy = \int \ \sin t \ ds = s\sin t + \cancelto{0}{C_2}\\ dz =\int \ s \ ds= \tfrac{1}{2}s^2 + \cancelto{0}{C_3}\\ \end{cases} $$ \(\implies \) $$ \begin{aligned} x(s,t) &= s\cos t \\ y(s,t) &= s\sin t \\ z(s,t) &= \tfrac{1}{2}s^2 \end{aligned} $$ Esto define la parametrización: $$ \Phi(s,t) = \big(s\cos t,\, s\sin t,\, \tfrac12 s^2\big). $$ Superficie suave construida a partir de EDOs parametrizadas5
Geométricamente, esta construcción muestra cómo una Inmersión diferenciable  puede obtenerse explícitamente a partir de ecuaciones diferenciales ordinarias. (Ver video Concepto de Inmersión Diferenciable)
Conclusión Un conjunto de ecuaciones diferenciales suaves define una curva o superficie suave cuando sus soluciones existen, son únicas y poseen vectores tangentes no degenerados. En términos generales, una curva suave en el plano puede describirse como la solución de un sistema de ecuaciones diferenciales del tipo: $$ \begin{cases} \dot{x}(t) = f(x(t), y(t)) \\ \dot{y}(t) = g(x(t), y(t)) \end{cases} $$ 
Si las funciones \(f\) y \(g\) son suaves (\(C^\infty\)), entonces las soluciones existen localmente, dependen suavemente de los parámetros y generan curvas suaves. En geometría diferencial, el punto \(x(t)\) pertenece a la variedad \(M\), mientras que \(\dot{x}(t)\) representa un vector tangente en ese punto, es decir, \[ \dot{x}(t) \in T_{x(t)}M. \]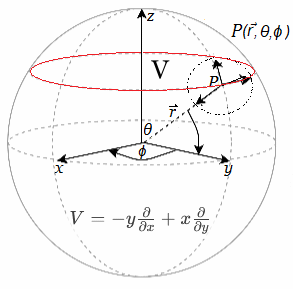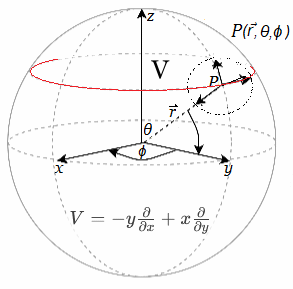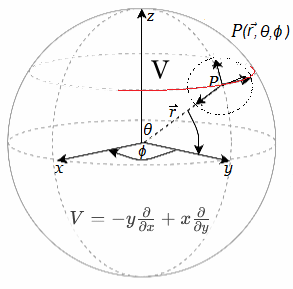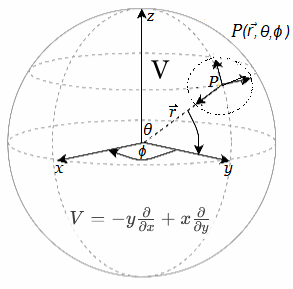 
Campo Vectorial Alredor Esfera6 Así, cada curva induce de manera natural un campo de vectores tangentes a lo largo de su trayectoria. Anexo ~ Parámetros \(t \longrightarrow s\) Al parametrizar una curva en el espacio se simplifica su descripción desde el uso de coordenadas cartesianas \((x,y,z)\) hacia el parámetro \(t\). Así mismo, se facilita la incorporación vectorial de la representación.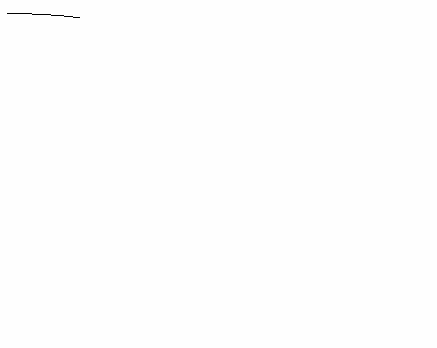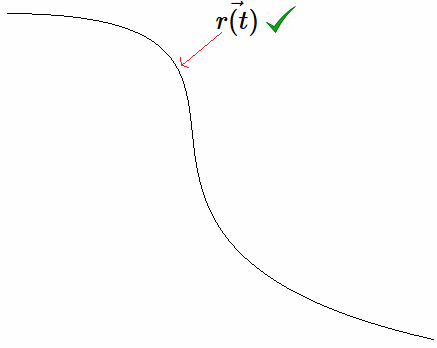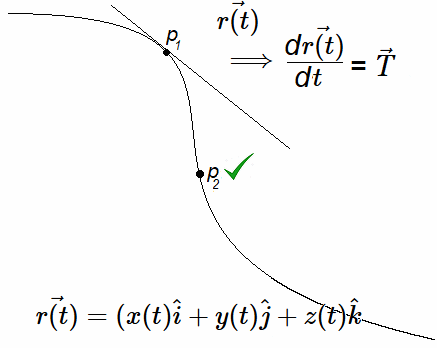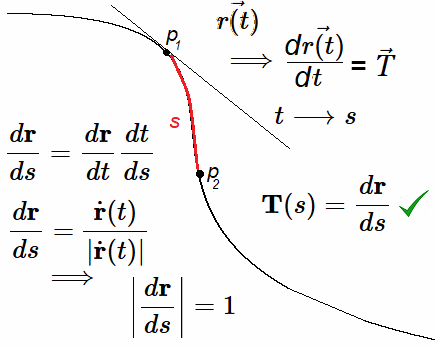 
En efecto, sea $$ \vec{r(t)}=(x(t)\hat{i} + y(t)\hat{j} + z(t)\hat{k} $$ donde \(t\) es un parámetro - no necesariamente el tiempo. El significado geométrico real del cambio $$ t \longrightarrow s $$ La curva paramétrica en \(C\) en \(\mathbb{R}^3\) es suave: $$ \mathbf r(t) = (x(t), y(t), z(t)), \qquad t \in [a,b] $$ Aquí:
∘ No mide distancia. ∘ Puede acelerar, frenar o retroceder. Dos valores distintos de \(t\) no implican recorrer la misma longitud de curva. El parámetro geométrico de la longitud de arco desde \(t=a\) hasta \(t\) se define como: $$ s(t) = \int_a^t |\dot{\mathbf r}(u)| du $$ Donde se define una nueva variable $$ s = s(t) $$ con las siguientes propiedades:
∘ \(s\) mide distancia real sobre la curva. ∘ Es intrínseca, no depende del parámetro original. Luego, el cambio de parámetro \(t \to s\), cuando la curva es regular: $$ |\dot{\mathbf r}(t)| \neq 0 $$ entonces:
∘ Se puede invertir: $$ t = t(s) $$ Esto permite reparametrizar la curva: $$ \mathbf r(s) := \mathbf r(t(s)) $$ Entonces, derivando respecto de \(s\): $$ \frac{d\mathbf r}{ds} = \frac{d\mathbf r}{dt} \frac{dt}{ds} = \frac{\dot{\mathbf r}(t)}{|\dot{\mathbf r}(t)|} $$ $$\implies $$ $$ \left|\frac{d\mathbf r}{ds}\right| = 1 $$
∘ Las fórmulas mezclan geometría y parametrización.
∘ Las derivadas reflejan solo la forma geométrica. ∘ La curva se describe "a paso constante". Por eso, el vector tangente unitario es: $$ \mathbf T(s) = \frac{d\mathbf r}{ds} $$ En resumen:
∘ \(s\): distancia real sobre la curva. ∘ \(t \to s\): paso de descripción cinemática a geométrica. |
| DocIRS © 1988-2026 |
|
Notas Adjuntas
|
