| + Ficha Técnica |
| + Mapa Publicaciones |
| + Videos Asociados |
|
Introducción En este artículo se presenta, de manera introductoria, el concepto de inmersión dentro de la Geometría Diferencial1, incorporando además una breve referencia a las singularidades y a su relación con la Teoría de Lie, en particular con el Grupo Lineal Especial \(SL_2 \). 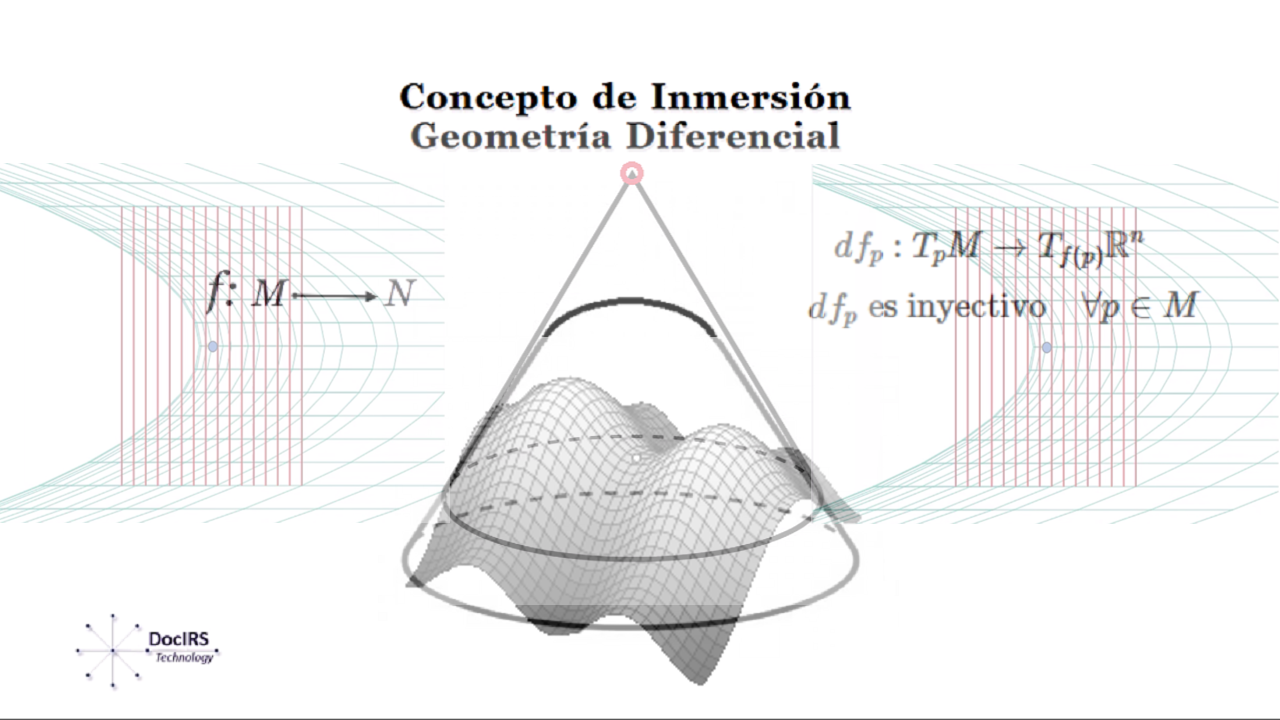Como material complementario, se utiliza el artículo "Ejemplo \(SL_2\) ~ Grupo Lineal Especial ~ Generadores del Algebra de Lie" y su video asociado 
 Ejemplo Sl2
~ Grupo Lineal EspecialRegularización de una singularidad ~ inmersión en \(SL_2,(\mathbb{R})\) En geometría diferencial, en ciertas situaciones es necesario obtener una superficie suave sobre un objeto geométrico, eliminando discontinuidades generadas por la presencia de puntos problemáticos (singularidades2). Estos puntos deben ser corregidos o "rellenados" mediante procesos de regularización que respeten la naturaleza geométrica de la superficie. Cuando el límite que define la continuidad no existe, la singularidad no puede eliminarse, y esto exige un rediseño de la inmersión involucrada3. ¿Qué es — y qué no es— una inmersión? Es importante aclarar algunos conceptos fundamentales:
Lo que suele generar confusión es distinguir dos niveles:
ii) La condición adicional sobre su diferencial \(df_p\). Una variedad diferenciable \(M\) es un espacio topológico4 que localmente se parece a \(\mathbb{R}^m\), y que viene equipado con un atlas que permite definir la diferenciabilidad de aplicaciones entre variedades5. Cuando se tiene un mapa \[ f : M \to N, \] lo primero que se exige para estudiarlo con herramientas de cálculo diferencial es que sea suave (diferenciable \(C^\infty)\).(Ver Grupos de Lie ~ Geometria_Diferencial y Ejemplo  )
Esa es la base: si un mapa no es diferenciable, ni siquiera se puede discutir su diferencial \(df\). - Una inmersión no implica singularidades. De hecho, ocurre lo contrario: es un mapa cuyo diferencial es inyectivo en todos los puntos, evitando comportamientos degenerados. - Una inmersión no garantiza que su imagen sea una subvariedad embebida. La imagen puede plegarse, autointersectarse o no ser una superficie en el sentido topológico usual. En resumen, una inmersión preserva completamente la estructura local de la variedad. Localmente, siempre se ve como una copia suave de la variedad original dentro de un espacio ambiente mayor. Ejemplos de Inmersión
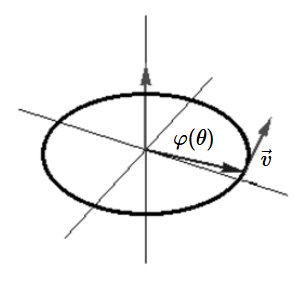 Variedad dentro de un Espacio Mayor \[ \varphi : S^1 \hookrightarrow \mathbb{R}^2, \] \[ \varphi(\theta) = (\cos\theta, \sin\theta) \] Es suave, dado que su diferencial es: \[ \frac{d\varphi}{d\theta} = (-\sin\theta, \cos\theta) \] Este vector \(\vec{v}=(-\sin\theta, \cos\theta)\) nunca es cero, por lo que el diferencial es inyectivo. Luego, es una inmersión. Nótese que localmente el círculo parece una línea, la imagen es invariante, no se pierde dimensión. 2.- Mapa suave de paraboloide sobre dominio malla: \[ F(x,y) = (x, y, x^2 + y^2) \]. El jacobiano tiene rango \(2\) en todos los puntos \(\longrightarrow \) inmersión.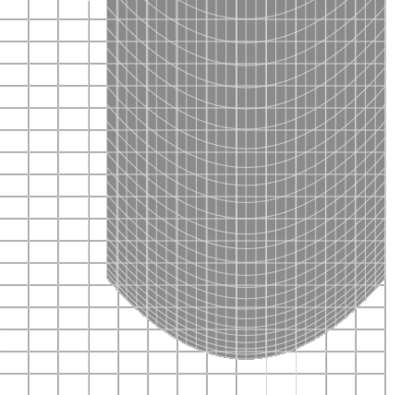 
Inmersión en \(\mathbb R^2\): Imagen suave y no colapsada en la superficie. Ejemplo NO Inmersión (Singularidad)
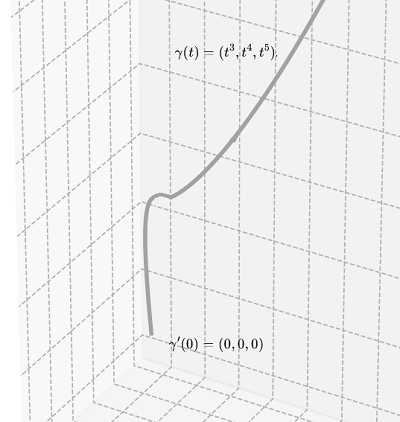 Curva inserta en espacio euclidiano NO inmersión \[ \gamma(t) = (t^3, t^4, t^5) \] \[\implies\] \[ \frac{d\varphi}{dt}=\gamma'(t) = (3t^2, 4t^3, 5t^4) \] 2.- Mapa con degeneración en el origen: \(G(x,y) = (x^2 - y^2, 2xy, x^2 + y^2) \). En \((0,0)\) el jacobiano se anula \(\longrightarrow \) la derivada no es inyectiva y la imagen presenta un punto "colapsado".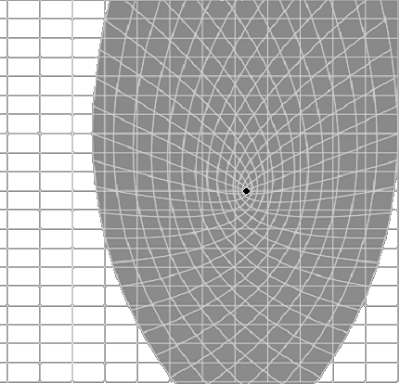 
Punto singular en \(\mathbb R^2\): Mapa con colapso en el origen (singularidad). Los ejemplos en el marco de la Geometría Diferencial muestra que una imersión diferenciable se entiende como una aplicación suave (continuamente derivable) que introduce un objeto geométrico de menor dimensión dentro de un espacio de mayor dimensión sin colapsar direcciones, es decir, preservando la "estructura local" del dominio. Definición Formal de imersión diferenciable Sea \[f : M \to \mathbb{R}^n\] Una aplicación de clase \( C^1 \) (o más suave). Decimos que \( f \) es una inmersión si su diferencial es inyectivo en todos los puntos: \[ df_p : T_p M \to T_{f(p)}\mathbb{R}^n \] Esto significa que: - La aplicación no aplasta, no dobla en ángulos infinitos ni pierde dimensiones. - Localmente, la imagen de \(M\) se ve como una copia suavizada de la variedad original dentro del espacio \( \mathbb {R}^n\). Geométricamente se interpreta como Si \(M\) es, por ejemplo, una superficie bidimensional y la inmersión es \[ X(u,v) : U\subset\mathbb{R}^2 \to \mathbb{R}^n, \] Entonces: - La superficie queda suavemente colocada dentro de \(\mathbb{R}^n\). - No aparecen pliegues con esquinas ni rupturas. - Los vectores tangentes se transforman de manera coherente y sin colapsar. Desarrollo Concepto de Inmersión A partir de los ejemplos previos sobre inmersiones y singularidades, y considerando la definición formal de inmersión, se presenta ahora un desarrollo más profundo de estos conceptos mediante el estudio de una superficie suave que contiene un cono con punta. El objetivo es mostrar cómo eliminar dicha singularidad mediante un proceso de regularización, obteniendo finalmente una inmersión suave en \(SL_2,(\mathbb{R})\). Para ello, se explica cómo la derivada de esta inmersión permite describir un espacio tangente en términos del álgebra de Lie asociada, \(\large{\mathfrak{g = sl_2}}\).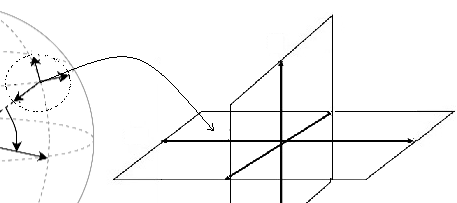 
Variedad Superficie (carta)\(\longrightarrow\) Plano Cartesiano La idea principal es evitar la discontinuidad presente en la punta del cono y obtener una superficie realmente suave, es decir, una variedad diferenciable. Para ello es necesario eliminar el punto en el que la función de inmersión deja de ser continuamente derivable. Esto se consigue garantizando que la aplicación que mapea la superficie hacia un espacio euclidiano sea completamente diferenciable y no presente singularidades. En términos de geometría diferencial, esto implica que la transformación debe ser suave y que sus derivadas no se anulen en ningún punto relevante, asegurando así la regularidad de la inmersión.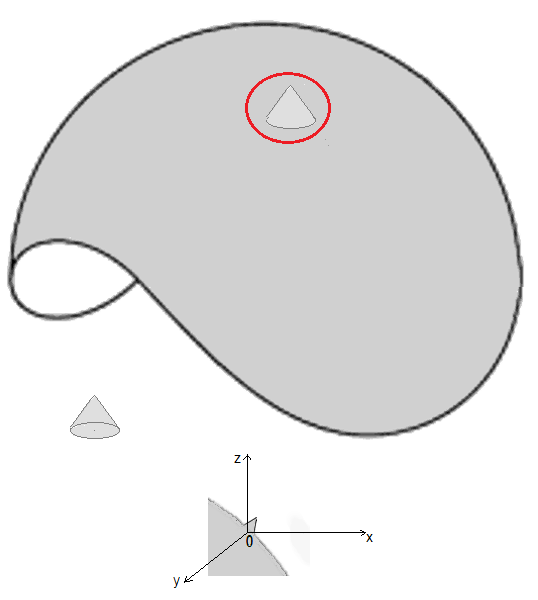 
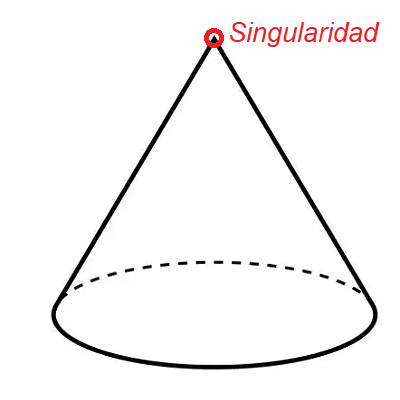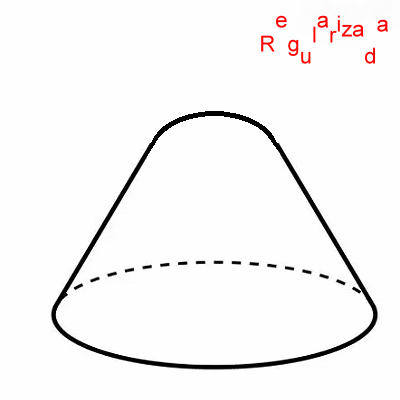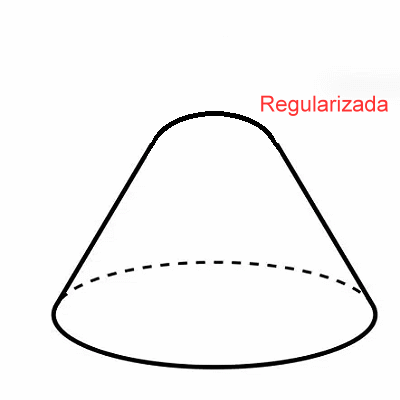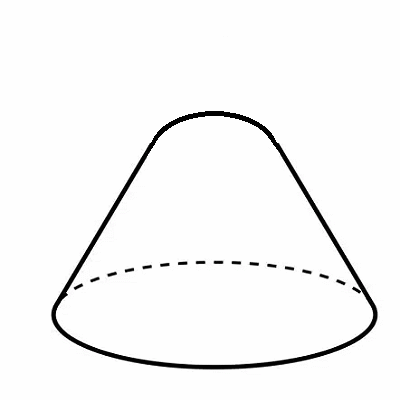
Cono con punta sobre una Superficie Suave Es decir, se tiene un objeto suave "casi diferenciable" que contiene un cono \(C\) estándar en \(\mathbb{R}^3\): 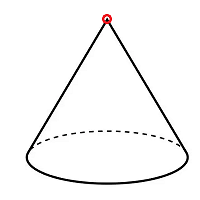$$ C=\{(x,y,z)\in\mathbb{R}^3: $$ $$ z^2 = x^2 + y^2\}. $$ Este conjunto es suave fuera del vértice \((0,0,0)\), pero no es una variedad diferenciable, i.e. no es continuamente derivable, dado que la punta es una singularidad, donde la superficie no tiene un plano tangente bien definido en ese punto.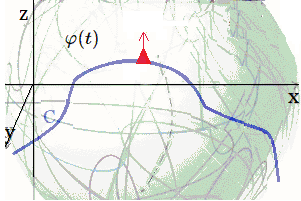 
Singularidad ~ \(\not \exists \) Plano Tangente Una regularización elemental (suavizado) del cono es: $$ C_\varepsilon=\{(x,y,z)\in\mathbb{R}^3: $$ $$ z = \sqrt{x^2 + y^2 + \varepsilon^2}\} $$ $$ \varepsilon>0 $$ En efecto, para \(\varepsilon>0\) la función \(z(x,y)=\sqrt{x^2+y^2+\varepsilon^2}\) es \(C^\infty\) en todo \(\mathbb{R}^2\), de modo que \(C_\varepsilon\) sí es una variedad diferenciable (superficie suave): la punta queda redonde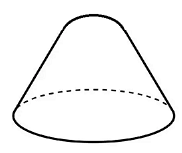ada. Esta idea de inmersión suave del objeto en \(SL_2,(\mathbb{R})\), - donde ya se estableció que \(SL_2,(\mathbb{R})\) es el grupo de matrices \(2\times 2\) reales con determinante \(1\) -. Es decir, \(SL_2,(\mathbb{R})\) es una variedad diferenciable de dimensión \(3\). (Ver deducción de los generadores del Algebra de Lie, Grupo \(\mathbf {SL_2 \longrightarrow}\) Algebra de Lie \(\mathfrak{\Large g = \large{\mathfrak{sl}_2}(\mathbb{R})}\))
Su álgebra de Lie \(\large{\mathfrak{sl}_2}(\mathbb{R})\) es el espacio tangente en la identidad, con conmutador (corchetes de Lie) tiene una base típica de generadores: \[ \Bigg\{ \underbrace{\begin{pmatrix} 0 & 1\\ 0 & 0\\ \end{pmatrix}}_{\large{\text{E}}} , \underbrace{\begin{pmatrix} 0 & 0\\ 1 & 0\\ \end{pmatrix}}_{\large{\text{F}}}, \underbrace{\begin{pmatrix} 1 & 0\\ 0 & -1\\ \end{pmatrix}}_{\large{\text{H}}} \Bigg\} \]
Contrucción Aplicación Suave Si se construye una aplicación suave6 $$ \mathit{\varphi} : M \to SL_2,(\mathbb{R}), $$ donde \(M\) es nuestra superficie regularizada, - por ejemplo \(C_\varepsilon\) parametrizada por \((r,\theta)\) -, entonces la imagen \(\mathit{\varphi}(M)\) será una subvariedad suave de \(SL_2,(\mathbb{R})\) siempre que \(\mathit{\varphi}\) sea una inmersión (es decir, que su derivada sea inyectiva en cada punto). Con ello convertimos el objeto en una variedad diferenciable inside \(SL_2,(\mathbb{R})\). Parametrizamos la superficie regularizada por coordenadas polares en el plano base: $$ r\ge 0,\qquad \theta\in[0,2\pi),$$ $$ X(r,\theta) = (x,y,z) = \big(r\cos\theta,\; r\sin\theta,\; \sqrt{r^2+\varepsilon^2}\big). $$ Se define una función suave \(u(r,\theta)\in\large{\mathfrak{sl}_2}(\mathbb{R})\) y luego usar la exponencial matricial: $$ \mathit{\varphi}(r,\theta) \;=\; \exp\big(u(r,\theta)\big) \in SL_2,(\mathbb{R}). $$ Una elección simple y didáctica es, en la base \(E,F,H\), $$ u(r,\theta) \;=\; \varphi(r)\big(\cos\theta\,E + \sin\theta\,F\big) \;+\; \psi(r)\,H, $$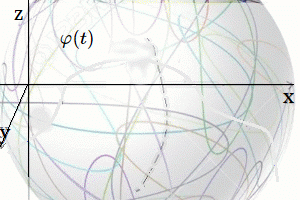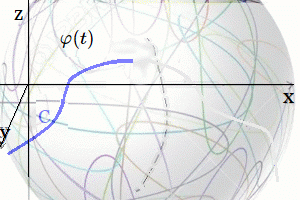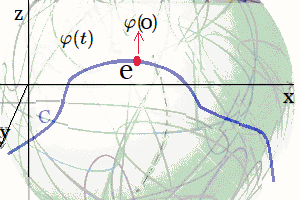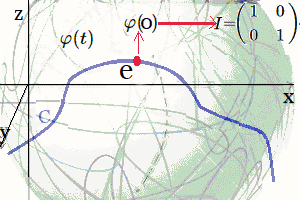 
Curva Continua Superficie Suave donde \(\varphi,\psi\) son funciones suaves con \(\varphi(0)=0,\ \psi(0)=0\). Esto asegura que \(u(0,\theta)=0\) y por tanto \(\mathit{\varphi}(0,\theta)=I\), evitando una singularidad en la imagen. Ejemplo Aplicación Suave $$ \varphi(r)=\frac{r}{1+r},\qquad \psi(r)=0,\quad\Rightarrow $$ $$ u(r,\theta)=\frac{r}{1+r}\big(\cos\theta\,E + \sin\theta\,F\big), $$ $$ \mathit{\varphi}(r,\theta)=\exp\big(u(r,\theta)\big). $$ Observaciones claves:
- Localmente la inmersión es suave y la derivada respecto a \(r,\theta\) puede ser de rango \(2\) si \(\varphi'(0)\neq0\). - Con elección adecuada de \(\varphi\), \(D\mathit{\varphi}\) tendrá rango \(2\) y \(\mathit{\varphi}\) define una superficie inmersa en \(SL_2,(\mathbb{R})\). - Geométricamente, colocamos una superficie suave en \(SL_2\) que representa la regularización del cono; la imagen no presenta vértice singular. Al regularizar a \(z=\sqrt{x^2+y^2+\varepsilon^2}\quad\)la superficie se vuelve \(C^\infty\). De modo que al pasar a \(SL_2,(\mathbb{R})\) mediante \(\mathit{\varphi} = \exp \circ u \quad \) con \(\quad u\) suave, la imagen es una superficie suave dentro de una variedad lisa de dimensión \(3\). No aparece la punta en la imagen. Donde la exponencial matricial \(\exp:\large{\mathfrak{sl}_2}\to SL_2\) es diferenciable, y en una vecindad de \(0\in\large{\mathfrak{sl}_2}\) la exponencial es localmente difeomorfismo, por lo que la regularidad se preserva.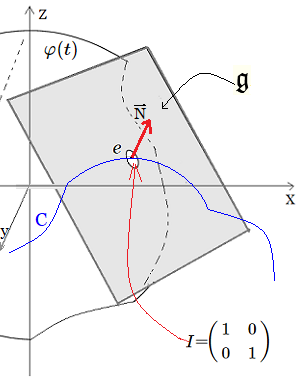 
Plano Tangente Sobre el Neutro~ Matriz Idéntica Ahora, sea \(p=\mathit{\varphi}(r_0,\theta_0)\in SL_2,(\mathbb{R})\). El espacio tangente \(T_p SL_2\) puede identificarse con \(\large{\mathfrak{sl}_2}\) mediante la traslación a la izquierda: $$ dL_{p^{-1}}:T_p SL_2\longrightarrow T_e SL_2=\large{\mathfrak{sl}_2}, $$ $$ v\mapsto (dL_{p^{-1}})_p(v). $$ La derivada de \(\mathit{\varphi}\) en \((r,\theta)\), $$ D\mathit{\varphi}_{(r,\theta)}:T_{(r,\theta)}(\text{parámetros})\simeq\mathbb{R}^2\longrightarrow T_{\mathit{\varphi}(r,\theta)}SL_2, $$ proporciona vectores tangentes a la imagen. Componiendo con \(dL_{\mathit{\varphi}(r,\theta)^{-1}}\) obtenemos su representante en \(\large{\mathfrak{sl}_2}\): $$ \xi = dL_{\mathit{\varphi}(r,\theta)^{-1}}\big(D\mathit{\varphi}_{(r,\theta)}(\partial_r)\big)\in\large{\mathfrak{sl}_2}, $$ $$ \eta = dL_{\mathit{\varphi}(r,\theta)^{-1}}\big(D\mathit{\varphi}_{(r,\theta)}(\partial_\theta)\big)\in\large{\mathfrak{sl}_2}. $$ Estos elementos de \(\large{\mathfrak{sl}_2}\) son la representación del espacio tangente de la superficie en el álgebra. Existe una fórmula útil para el diferencial de la exponencial (necesaria si \(\mathit{\varphi}=\exp\circ u\)): Si \(u(t)\in \mathfrak{sl}_2\) es una curva y \(A(t)=\exp(u(t))\) entonces: \[ \frac{d}{dt}A(t)=\exp(u(t))\cdot\Big( \frac{e^{\operatorname{ad}_{u(t)}}-I}{\operatorname{ad}_{u(t)}}\big(u'(t)\big)\Big), \] donde \(\operatorname{ad}_u(v)=[u,v]\). Así la correspondencia entre la derivada de los parámetros y un elemento de \(\large{\mathfrak{sl}_2}\) está dada por la aplicación lineal dependiente de \(u\): $$ \mathcal{L}_{u} := \frac{e^{\operatorname{ad}_{u}}-I}{\operatorname{ad}_{u}} \;:\; \large{\mathfrak{sl}_2} \to \large{\mathfrak{sl}_2}. $$Por tanto, si \(\mathit{\varphi}=\exp\circ u\) y tomamos \(v\in T_{(r,\theta)}\) con componente \(u'(v)\in\large{\mathfrak{sl}_2}\) (la derivada de \(u\) en la dirección \(v\)), entonces $$ dL_{\mathit{\varphi}^{-1}} \circ D\mathit{\varphi} (v) = \mathcal{L}_{u(r,\theta)}\big( u'(v) \big)\in\large{\mathfrak{sl}_2}. $$Cuando \(u\) es pequeño (por ejemplo cerca de \(r=0\)), \(\mathcal{L}_u\) es cercano a la identidad y la relación es sencilla: esto facilita identificar el espacio tangente de la superficie con un subespacio de \(\large{\mathfrak{sl}_2}\). Por tanto,
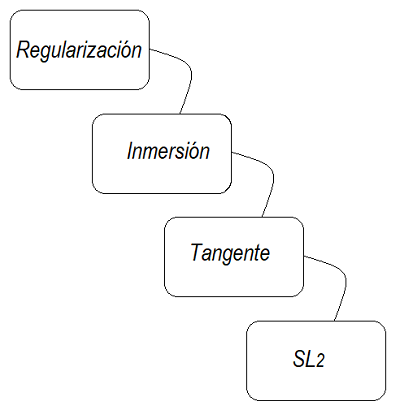
Síntesis: Patrón Estándar Esta construcción es un patrón estándar: cuando una superficie tiene una singularidad local, hay dos estrategias principales:
El uso del grupo \(SL_2\) y su álgebra \(\large{\mathfrak{sl}_2}\) permite una descripción algebraica del espacio tangente
(pues \(T_e SL_2=\large{\mathfrak{sl}_2}\)) y fórmulas explícitas (como \(\mathcal{L}_u\)) que relacionan derivadas paramétricas con
elementos del álgebra —ideal para conectar la geometría diferencial con la teoría de Lie.
|
|
Notas Adjuntas
|
| DocIRS © 1988-2025 |
