Algebra de Lie $Mn(K)$ - Aplicaciones ~ Formalización
La intención de este capítulo, - previo a la definición formal del Algebra de Lie -, es precisar una introducción a la
teoría del Algebra de Lie, mediante la descripción de herramientas básicas, tales como el grupo multiplicativo de los complejos diferente de Cero ($C^{*}$), distinguir el producto interno del espacio vectorial complejo, tratar la operación binaria Corchetes de Lie con Levi-Civita, señalar cómo se deriva hacia los grupos especiales y unitarios de Lie $SU(n)$87, de igual manera, explicar la idea de las variedades diferenciables y esbozar ciertas aplicaciones en robótica.
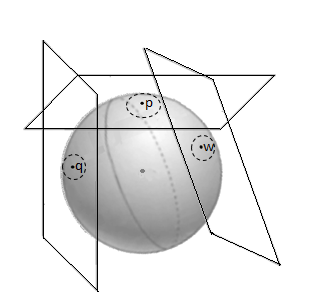
Planos Tangentes ~ Puntos Superficie de una Esfera118
Sea M una variedad topológica de dimensión $\mathit{n}$. Una carta o vecindad abierta en $M$ es un par $(U,\varphi)$, donde $U$ es un abierto de $M$ y $\varphi: U \rightarrow \varphi(U)=\hat{U}$ es un homeomorfismo de $U$ al abierto $\hat{U}$ de $\mathbf{R}^n$. La transformación $\mathit{\varphi}$ se le suele llamar cambio de coordenadas o función de transición.
Nótese que una variedad localmente tiene propiedades hereditarias del espacio euclídeo, pero no así con las propiedades globales. Por eso es necesario agregar condiciones globales a la definición, a fin de evitar excepciones. De ahí que, la definición de variedad topológica garantiza que $\forall p \in M$, es posible encontrar una carta $(U,\varphi)$, tal que $\mathit{p}$ esté en su dominio.
Ahora, si $\mathit{\varphi(p)}=0$ se dice el centro de la carta es $\mathit{p}$. (Sacando el vector constante $\mathit{\varphi(p)}$).
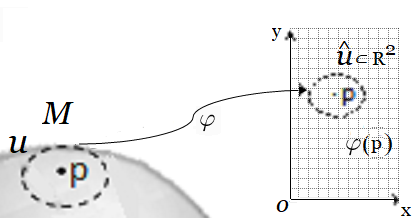
Variedad Superficie Esfera (carta) - Plano Cartesiano
Equivalencia Topológica ~ Homeomorfismo
En la búsqueda de encontrar funciones existentes continuas y biunívocas entre espacios, tenemos desde la trigonometría el ejemplo de la función tangente. Restringiendo su dominio a un intevalo abierto de los propios reales:
Ciertamente, el intervalo abierto $U=]-\frac{\pi}{2}, +\frac{\pi}{2}[$, que es un subconjunto de los reales, se dice que es topológicamente equivalente al conjunto de todos los reales, dado que existe al menos una función continua y biyectiva $\mathbf{\varphi}$ entre estos dos conjuntos.
Esto, los convierte en espacios homeomorfos116, i.e. $\forall x\in U \text{ }\exists \mathbf{\varphi(x)}\in R$. Además con $\mathbf{\varphi(x)}=0$ la carta o vecindad está centrada en $\mathbf{x}$.
En efecto,la función:
$$\mathbf{\varphi}:]-\frac{\pi}{2}, +\frac{\pi}{2}[\subset R\quad \longrightarrow \quad ]-\infty,+\infty[=R\quad \text{, donde } \mathbf{\varphi(x)}=tan(x)$$
Nótese que
$$x \longrightarrow -\frac{\pi}{2}\quad \Rightarrow \mathbf{\varphi(x)}\longrightarrow -\infty \\
x=0 \quad \Rightarrow \mathbf{\varphi(x)}=0 \\
x \longrightarrow +\frac{\pi}{2}\quad \Rightarrow \mathbf{\varphi(x)}\longrightarrow +\infty$$
El arcotangente es la función inversa de la tangente. Es decir, $\mathbf{\varphi^{-1}}(x)=arctan(x) \iff x=tan(\varphi(x))$.
|
|
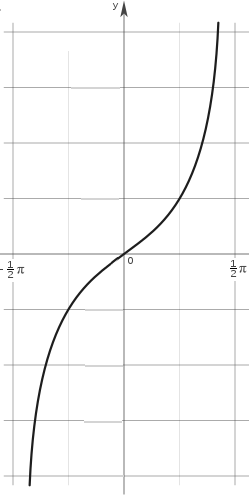
$]-\frac{\pi}{2}, +\frac{\pi}{2}[ \longrightarrow R$
|
Equivalencia Topológica ~ Isomorfismo
La equivalencia topológica denominada isomorfismo se distinque de un homeomorfismo cuando se trabaja sobre variedades suaves. En ese ámbito todos los isomorfismos son homeomorfismos, no así al contrario. Un homomorfismo es simplemente un isomorfismo que no es biyectivo.(Puede ser no suprayectivo)
Supongamos $G$ y $H$ son grupos. Entonces se dice que $\varphi:G \longrightarrow H$ es un isomorfismo de grupos si $\varphi$ es bijectiva (i.e., $\varphi$ es inyectiva(1-1) y suprayectiva (sobre), donde se satisfacen las tres siguientes condiciones:
- i) $\varphi(e) = e$, donde $e$ es el elemento neutro.
- ii) $\varphi(g^{-1}) = \varphi(g)^{-1} \ \forall \ g \in G$
- iii) $\varphi(gh) = \varphi(g)\varphi(h) \ \forall \ g,h \in G$
|
En síntesis, $\varphi(a*b)=\varphi(a)·\varphi(b)\Rightarrow \forall a,b \in G$. Luego, la transformación $\varphi()$ preserva la operación de grupo. Además, para grupos finitos significa que $G$ y $H$ tienen el mismo tamaño y que para todo elemento de $G$ existe un único elemento en $H$
Varios de los fundamentos de esos conceptos se trataron en los capítulos previos del documento Puertas de Pauli y Algebra de Lie, y sus videos complementarios que intentan describir sus resultados más significativos.
El enfoque que aquí se expone es clásico y simple. El tema está profunda y abundantemente documentado en centenas de artículos académicos de Matemáticas108, Mecánica Cuántica, y diversas disciplinas científicas e ingenieriles.
Es decir, existe una serie de tópicos atingentes que están lejos de los propósitos de este capítulo, el cual pretende formalizar
el Algebra de Lie, a partir del uso de las Matrices de Pauli. Por tanto, en el presente artículo se tocan una serie de conceptos matemáticos involucrados como Topología, Variedades Diferenciables, Teoría de Grafos, u otras ramas complejas de la matemática que son brevemente tratados, en tanto introducción de introducciones. (Ver artículo: Definición Algebra de Lie ~ Variedad Diferenciable  ). ).
Aplicación del Algebra de Lie
Breve Preámbulo

Ejemplo de Homeomorfismo ~ La misma agua Vaso-Plato
Equivalencia topológica116
La aplicación del Algebra de Lie obliga a todos aquellos que trabajan en programación, desarrollo de sistemas y robótica a equiparse con más matemática. Especialmente a profundizar en el Algebra Lineal en el campo de las transformaciones lineales y un poco de Topología. Dicho de otra manera, avanzar en el concepto de espacio Euclidiano, donde cada punto $p \in M\subseteq R^2$, tiene una vecindad que es homeomorfa (función de un espacio topológico a otro) en un subconjunto abierto en $R^n$. Esta propiedad lo convierte en una variedad diferenciable117.
Una introducción simple al concepto de variedad topológica unidimensional es la relación entre una línea y un círculo. Se entiende que la topología hace abstracción del arco (curvo) y de sus propiedades métricas. (Ver Propiedades Geométricas Cualitativas). Donde un segmento de un círculo se transforma mediante una función $\varphi()$ en una línea. Es decir, es un mapeo continuo e invertible desde $R^2$ hacia el intervalo abierto $]-1,1[$ en $R$
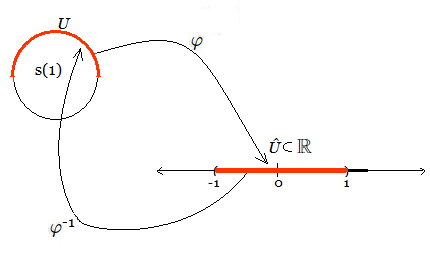
Ejemplo: Variedad o Manifold Suave
Luego, el concepto topológico de variedad bidimensional es un abstracción matemática del cotidiano concepto de superficie, que conocemos en un hoja de papel, un tabla delgada de madera, un lamina metálica, un banda rectangular, etc.. Es decir, estos objetos topológicos responden a la Geometría Euclidiana. Lo interesante es que la comprensión y extensión a espacios $R^n$ del concepto de variedad, se realiza a través de superficies. Nótese que la ventaja de la generalización de $R^2 \longrightarrow R^n$, es que todas las versiones de $R$ tienen la misma estructura topológica.

 |
 |
 |
 |
| Hoja de Papel |
Tabla de Madera |
Lamina Metálica |
Banda de Cartulina |
Ahora, los espacios de dimensiones superiores equivalentes a una $n \text{-variedad}$, son espacios topológicos con las mismas propiedades euclídeas. Esto significa que $R^n$ preserva las mismas propiedades estructurales topológicas de la variedad, dado que $R \subset R^2 \subset R^3 \dots \subset R^n$.
En el presente y en los diferentes artículos que hemos mencionado variedades, nos referimos a variedades compactas (y suaves), - generalmente de $2 \times 2$ -, basándonos en la existencia del teorema de clasificación de variedades compactas de dimensión $2$ [B59]. Teorema que facilita la comprensión y descripción de esta matemática topológica.
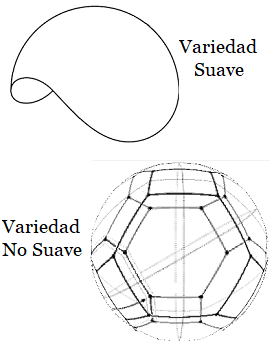
Variedad Suave (o lisa) vs Variedad No Suave (quebrada)
Obsérvese que un punto en una superficie curva o plana de un espacio vectorial, tiene una vecindad de puntos que lo transforma en una estructura topológica. Luego, mediante una función continua y biyectiva hacia una vecindad en otro espacio vectorial. Es decir, este mapeo es una variedad suave105.
La vecindad de un punto interior es un conjunto abierto de puntos próximos a él. Estos entornos pueden tener diversas clases (abiertos, cerrados, conexos, inconexos,...). Dentro de un Espacio Métrico, la unión de entornos puede cubrir un espacio. Así mismo, topológicamente puede definirse una métrica entre puntos interiores bajo propiedades cualitativas, i.e. no necesariamente distancias o cualidades numéricas.
Algebra de Lie y Robótica.
Con la aplicación del Algebra de Lie se puede describir y analizar el movimiento de robots, así como para controlar y planificar sus trayectorias.
Los robots son máquinas diseñadas para realizar tareas repetitivas. Para controlar estos robots de manera precisa y eficiente, se utiliza en parte el Algebra de Lie en los algoritmos, con otras tecnologías de control de movimientos.
(Ver Ejemplo de Aplicación - Generadores de Algebra de Lie $SO(3)$ -Control de Orientación en un Dron)
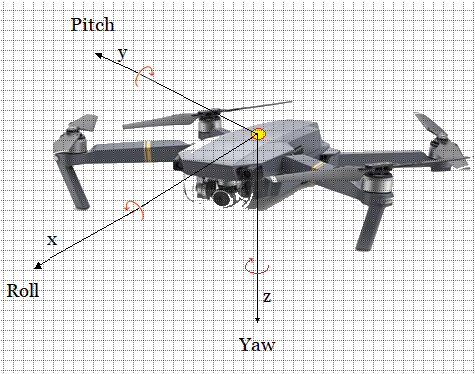
Ejemplo Dron: Vehículo Aéreo no Tripulado
Tal como se señala en un párrafo posterior la relación matemática entre las variables de articulación, la posición y orientación se expresan transformaciones homogéneas en Algebra de Lie.
El control de movimiento se basa en cálculos Jacobianos163, que son matrices relacionadas con el Algebra de Lie.
Estas matrices Jacobianas relacionan los cambios en los ángulos de Euler187 con los cambios correspondientes en la matriz de rotación. Las matrices Jacobianas establecen la relación entre sistemas de referencia.
Con una matriz Jacobiana $\large J$ es posible aplicar una rotación infinitesimal sobre un punto $P$ alrededor de los ejes $x, y, z$, y usar las derivadas parciales para calcular cómo cambia la posición del punto.
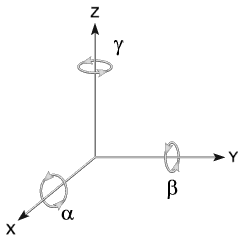
Rotaciones Independientes en Torno a Ejes188
Sea $R(\alpha,\beta,\gamma)=(R_{x},R_{y},R_{z})$, siendo la Jacobiana una matriz formada por las derivadas parciales de primer orden (todos balores escalares) de una función:
$$
\large{J_R}=\begin{pmatrix}
\frac{\partial R_{x}} {\partial \alpha} && \frac{\partial R_{x}} {\partial \beta} && \frac{\partial R_{x}} {\partial \gamma}\\
\frac{\partial R_{y}} {\partial \alpha} && \frac{\partial R_{y}} {\partial \beta} && \frac{\partial R_{y}} {\partial \gamma}\\
\frac{\partial R_{z}} {\partial \alpha} && \frac{\partial R_{z}} {\partial \beta} && \frac{\partial R_{z}} {\partial \gamma}\\
\end{pmatrix}
$$
Por ejemplo, para una rotación infinitesimal alrededor del eje $z$, podemos escribir:
$$
\frac{\partial P}{\partial \alpha} = \frac{\partial R}{\partial \alpha}\times P
$$
Donde $\frac{\partial P}{\partial \alpha}$ es el cambio infinitesimal en la posición del punto $P$ debido a una rotación infinitesimal alrededor del eje $z$, $\frac{\partial R}{\partial \alpha}$ es la matriz jacobiana de la rotación con respecto al ángulo $\alpha$, y $P$ es la posición original del punto $P$.
Cuando se trabaja con $SO(3)$, generalmente se enfrenta a parámetros que describen la rotación, como ángulos de Euler, ejes de rotación o cuaterniones.
Para entender cómo estos parámetros afectan una rotación particular, se utiliza la matriz jacobiana $J$.
En este caso, la forma de aplicación de $J$, es sobre matrices de rotación $R$ en $SO(3)$, siendo $SO(3)$ es el conjunto de todas las matrices de rotación $R_{3\times3}$, que cumplen las propiedades
i) $det(R) = 1$, asegura que no haya reflexiones involucradas en la rotación.
ii) $R^T·R = I$, donde $I$ es la matriz de identidad, i.e. garantiza que la matriz sea ortogonal.
$$\Rightarrow$$
| $$SO(3)=\unicode{123}R \text{ / }det(R)=1 \land (R·R^T=R^T·R=I)\unicode{125}$$ |
La matriz jacobiana $\large{J}$ de estas funciones se verá de la siguiente manera:
$$\large{J}=\frac{\partial R}{\partial \theta}$$
Donde $\partial R$ es el cambio infinitesimal en la matriz de rotación $R$ debido a un cambio infinitesimal en los parámetros $\theta=\unicode{123}\alpha,\beta,\gamma\unicode{125}$, los cuales describen la rotación.
La matriz jacobiana $\large{J}$ indica cómo las infinitesimales variaciones en los parámetros se traducen en pequeñas variaciones en la matriz de rotación. Esta información es crucial en aplicaciones de control, visión por computadora, robótica y muchas otras áreas en las que necesitas comprender cómo las rotaciones responden a cambios en los parámetros.
Por tanto, la matriz jacobiana se utiliza en el contexto de $SO(3)$ para describir cómo las pequeñas variaciones en los parámetros que definen una rotación se traducen en pequeñas variaciones en la matriz de rotación, lo que es fundamental en aplicaciones donde se requiere un control preciso de las rotaciones en el espacio tridimensional.
En resumen, al utilizar las derivadas parciales de la matriz de rotación con respecto a los ángulos de Euler, podemos calcular cómo cambia la posición de un punto en el espacio tridimensional cuando se aplica una rotación específica.
Esto es útil en aplicaciones donde se requiere el conocimiento de las transformaciones espaciales y sus efectos sobre los puntos en el espacio.
El diseño y desarrollo de algoritmos de control de movimiento permitirán que el robot se mueva a una posición y orientación programada mediante argumentos paramétricos de sus funciones.
Para definir trayectorias suaves y seguras para el robot, se utilizan técnicas de interpolación y optimización basadas en el Algebra de Lie. Esto implica encontrar el camino más corto o más eficiente entre dos puntos en el espacio de configuración del robot.
Durante la operación en tiempo real, el Algebra de Lie se usa para calcular y ajustar continuamente las velocidades de las articulaciones de un robot para describir la trayectoria de la función establecida. Esto garantiza que el robot realice su tarea con precisión y se adapte a cambios en el entorno.
-
Proceso de cálculo Matriz Jacobiana
El proceso de cálculo de la matriz jacobiana implica los siguientes pasos:
i) Definir una función vectorial que relaciona los parámetros de entrada con la matriz de rotación de salida. Esta función toma los parámetros como entrada y produce la matriz de rotación $R$ como salida.
ii) Expresar las pequeñas variaciones en los parámetros de entrada como un vector pequeño $\vec{\Delta\theta}$. Por ejemplo, si tienes un parámetro de ángulo $\theta$, la variación $\vec{\Delta\theta}$ sería un pequeño cambio en ese ángulo.
$$
\partial \theta=\lim_{n\to\infty} \left(\frac{\theta}{n} \right)
$$
iii) Calcular las variaciones correspondientes en la matriz de rotación $\Delta R$.
iv) La matriz jacobiana $\large J$ es una matriz que relaciona $\vec{\Delta\theta}$ y $\Delta R$. Cada elemento de la matriz $\large J$ se calcula tomando la derivada parcial de cada componente de la matriz de rotación $R$ con respecto a cada parámetro de entrada. En otras palabras, cada elemento $r_{i, j}$ de la matriz jacobiana $\large J$ se calcula como:
$$
\large J_{ij} = \frac{\partial R_{ij}}{\partial j}\\
\text{cuando, } \Delta \theta\longrightarrow 0 \Rightarrow \Delta R \longrightarrow 0
$$
v) Una vez que hayas calculado todos los elementos de la matriz jacobiana, tendrás una matriz que describe cómo pequeñas variaciones en los parámetros de entrada $\vec{\Delta\theta}$ se traducen en pequeñas variaciones en la matriz de rotación $\Delta R$. Esto es particularmente útil en aplicaciones de control, donde necesitas ajustar una rotación en respuesta a cambios en los parámetros.
Robótica
La aplicación del Algebra de Lie y su empleo creciente en el ámbito de la robótica (Ver Lie theory for the roboticist, Joan Solà112), particularmente la matemática de las rotaciones basada en cuaterniones.
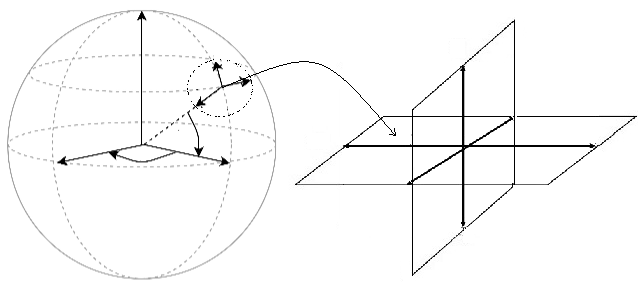
Variedad114 de $R^3 \longrightarrow R^2$
Esta relación de las operaciones en el grupo como muestra la figura "Variedad de $R^3 \longrightarrow R^2$" , que es curvo y no lineal, tienen un equivalente en el Algebra de Lie, que es un espacio vectorial lineal.
Nótese que, en la esfera, - como por ejemplo Esfera de Bloch -, definida en $R^3$ no constituye un grupo de Lie, sólo se utiliza como una representación gráfica, dado que en $R^4$ se describe el grupo de cuaterniones unitarios111.
El Algebra de Lie se incorpora a la robótica mediante los algoritmos de computación en el software de la máquina. Conjunto de aplicaciones y componentes desarrolladas en algún lenguaje de programación (C#, Python, javascript, asp, php,..) -, que gestionan el sistema sensorial del robot.
Estos algoritmos que aplican Algebra de Lie incluidos en el software, se utilizan en numerosos casos de robótica móvil (o cinemática), para mover estructuras mecánicas en la ejecución de tareas específicas.
La aplicación del Algebra de Lie en Robótica tiene múltiples beneficios, que se resumen en los siguientes tópicos:
- Precisión en el control de movimiento.
- Capacidad de adaptación a obstáculos o perturbaciones.
- Planificación de trayectorias eficientes y suaves.
- Posibilidad de trabajar en entornos peligrosos o inaccesibles para los humanos.
- Aumento de la productividad y la calidad en aplicaciones industriales.
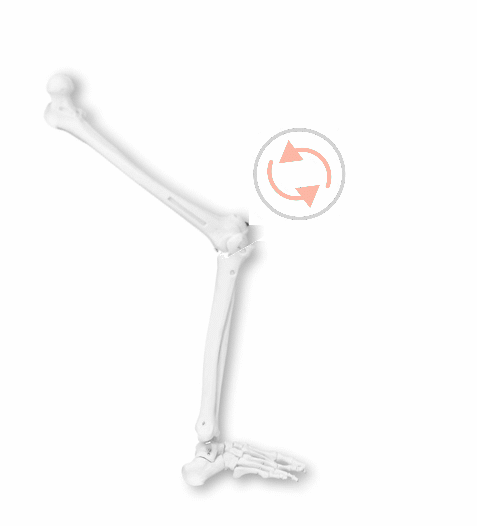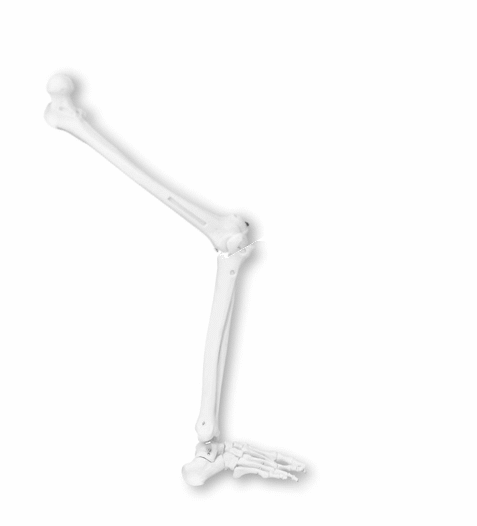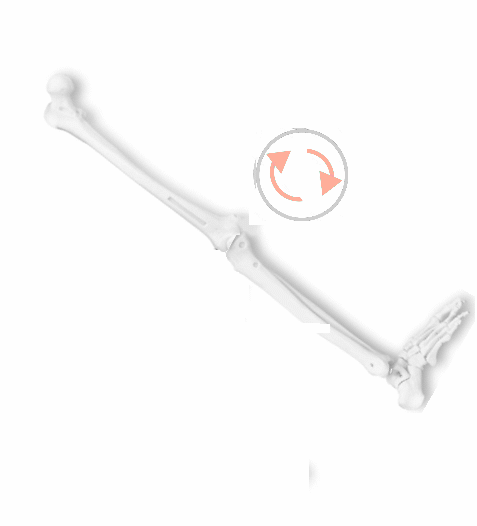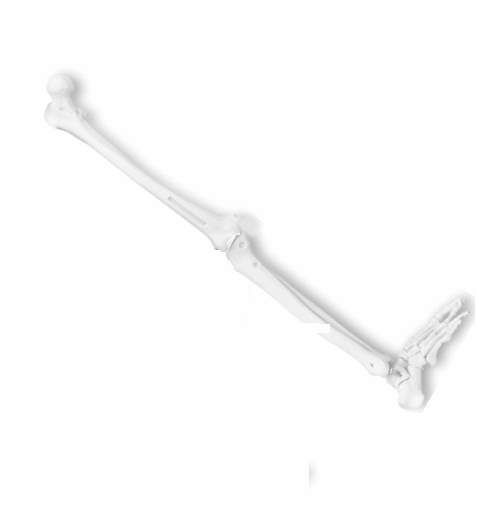
Rotación Rodilla-Tibia Humana
Nótese que dentro de la serie de artículos y videos acerca de álgebras y grupos de Lie que he publicado123, sólo me he enfocado desde la rotación de un objeto en torno a un punto de origen. Es decir, sin incluir aún los grupos de traslaciones en $R^n$, que ciertamente juegan un rol importantísmo en la robótica124.
Posicionamiento Brazo Robótico~Plano Cartesiano
Con álgebras de Lie es posible determinar los movimientos del brazo robótico, dentro de un espacio cerrado de operaciones, permitiendo calcular los ángulos de articulación necesarios para alcanzar una posición y orientación, - programada -, con precisión y eficacia.
Particularmente con Algebra de Lie de $SO(3)$, dentro de un espacio vectorial tridimensional que puede describir el movimiento de rotación del manejador o manipulador, el cual actúa con exactitud en la colocación de un dispositivo o efector de extremo. La pinza ('grippers') por ejemplo.
El Algebra de Lie del Grupo Euclídeo, describe las traslaciones en el espacio euclidiano tridimensional. En $SO(3)$ no existen traslaciones, solo se incluyen matrices $3\times 3$ ortogonales con determinante +$1$, que describen orientaciones.
Una traslación $\mathbf{p} \in \mathbb{R}^3 $ no pertenece a $SO(3)$, sino al grupo extendido de movimientos rígidos en $3$D, llamado Grupo de Lie $SE(3)$ (Special Euclidean Group) que se define como una extensión de los grupos especiales ortogonales tridimensionales, que combina rotaciones y posiciones: $SE(3) = SO(3) \ltimes \mathbb{R}^3$.
Brazo Robótico SE(3)
Entonces,
- Rotaciones - (cómo se orienta la pinza o cada eslabón).
- Traslaciones- (desde dónde hasta dónde se mueve).
Estas transformaciones combinadas se representan matemáticamente por el Grupo de Lie $SE(3)$:
$$
SE(3)=\left\{
\begin{pmatrix}
R & \mathbf{p} \\[4pt]
\mathbf{0}^{T} & 1
\end{pmatrix}
\;\middle|\;
R\in SO(3),\ \mathbf{p}\in\mathbb{R}^{3}
\right\}
$$
Donde:
- $SO(3)$: Grupo de rotaciones 3D.
- $\mathbf{p}$: Vector de traslación (posición.)
- La matriz representa la posición del efecto final (la pinza).
Es decir, mediante su algebra $\mathfrak {se(3)}$ se puede manejar el movimiento y control de un brazo robótico con pinza, brazo compuesto de varios eslabones conectados por articulaciones, cuya pinza se puede posicionar con cierta orientación y tomar un objeto y rotarlo.
La operación corchete de Lie, propia del Algebra de Lie permite calcular los conmutadores de las transformaciones infinitesimales que describen el movimiento del manejador de control.
En general, un brazo robótico es un aparato mecánico programable diseñado para manipular objetos con exactitud. El posicionamiento de un brazo robótico en el plano cartesiano implica la especificación de sus coordenadas.
Métricamente la posición relativa de los eslabones, - los cuales son objetos rígidos-, unidos entre sí por articulaciones y que se encadenan secuencialmente dentro del plano cartesiano, cuyas coordenadas son fundamentales para señalar la posición y relaciones geométricas del brazo robótico.
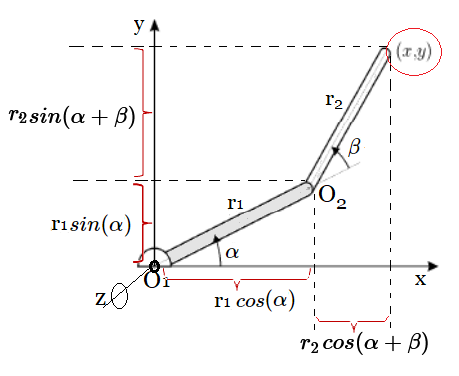
Posicionamiento ~ Brazo de 2 Eslabones
Es decir, la base del robot es un sistema de referencia fijo. De acuerdo a la figura previa,- que es un ejemplo de Cinemática Directa de un robot básico -, se observa:
- El origen $O_1$ en torno a cual gira el eslabón $r_1$ es $(0,0)$.
- El origen $O_2$ en torno a cual gira el eslabón $r_2$ es el extremo de $r_1$, i.e. $(r_1 \cos(\alpha),r_1 \sin(\alpha))$
- El extremo del eslabón $r_2$ tiene coordenadas $(x,y)$, que están determinadas por la suma de los segmentos, tanto en el sentido horizontal de eje de las $x$, como en el sentido vertical de las $y$.
- Los ángulos de rotación de ambos eslabones estarán dados por las condiciones de borde que se definan para el espacio de referencia donde funcione del robot.
- El sistema del brazo robótico de la figura tiene 2 grados de libertad.
Es decir, se asume que las articulaciones de brazo robótico le permiten moverse en distintas direcciones (dentro de determinados intervalos) y que cada articulación tiene un mecanismo eléctrico que puede girarlo hasta un ángulo determinado.
Dentro del Método Geométrico de Cinemática Directa, la localización extrema $(x,y)$ del brazo de este simple robot de dos eslabones está determinado por la siguiente expresión:
| $$
x=r_1·cos(\alpha)+ r_2·cos(\alpha + \beta)\\\\
y=r_1·sin(\alpha)+ r_2·sin(\alpha + \beta)\\
z=0
$$
|
| [AL_1] |
Donde se puede desagregar en dos matrices (y un escalar asociado que es la longitud del eslabón):
$$A_1=r_1\begin{pmatrix}
\cos(\alpha)\\
sin(\beta)\\
\end{pmatrix}\quad \land\quad
A_2=r_2\begin{pmatrix}
\cos(\alpha+\beta)\\
sin(\alpha+\beta)\\
\end{pmatrix}
$$
$$\begin{pmatrix}
x\\
y\\
\end{pmatrix}=A_1 + A_2
$$
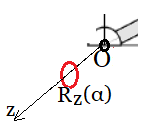
La expresión matemática de las ecuaciones [AL_1], representa la posición y orientación relativa entre los sistemas
asociados a dos eslabones consecutivos del robot.
Desde ahí, se puede configurar una matriz de transformación homogénea, dado que se tienen los valores de sus articulaciones y la matriz de rotación $R_z(\alpha)$, que se genera en torno al eje de las $z$ para su orientación.
|
|
|
|
|
Pausa
|
| |
Simulador - Desarrollo en Javascript 161
|
En efecto, las coordenadas $(x, y)$, son el punto final, donde interesa determinar su posición.
Este punto $(x,y)$ se calcula sumando las proyecciones de los eslabones o brazos sobre sus ejes cartesianos (Ver Figura Posicionamiento ~ Brazo de 2 Eslabones).
Por un lado, la coordenada $x$ es la suma de los dos segmentos en el sentido horizontal y lo mismo para la coordenada $y$ en el sentido vertical.
Nótese que las rotaciones del simulador constituyen un Grupo de Lie en los números reales (Ver Grupo de Lie-Enfoque Geométrico), dado que es un conjunto cerrado de rotaciones, con invariabilidad de la métrica, ortogonal, con determinante diferente de cero, asociativo, con elemento neutro e inversa. Además, continuo.
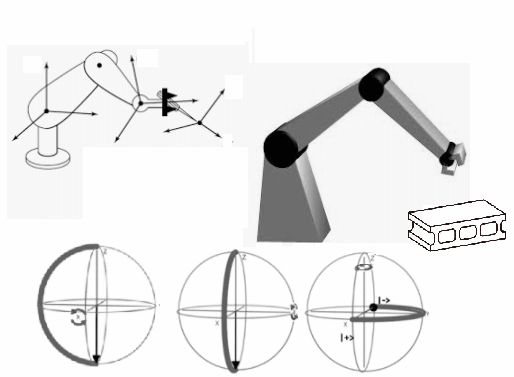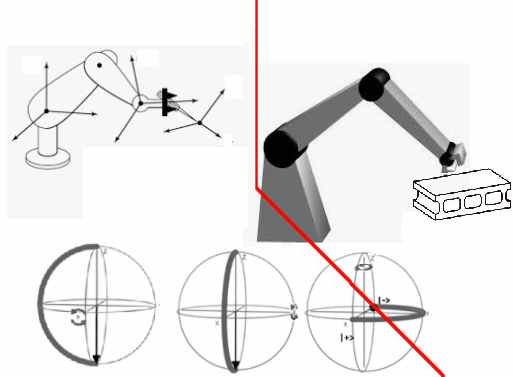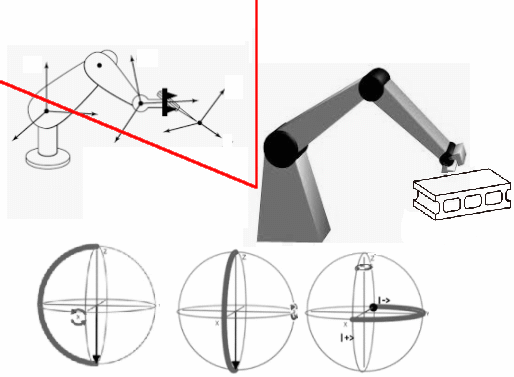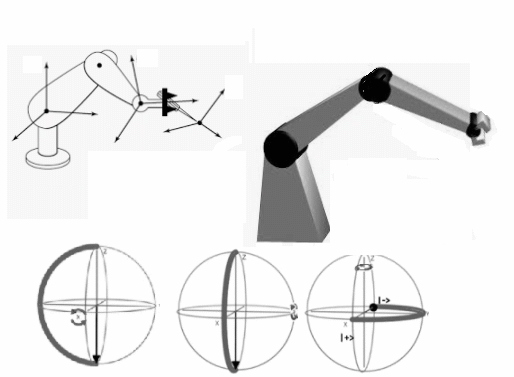
Rotación Matrices Homogéneas en $R^3$
Es necesario mencionar que dentro de las posibles aplicaciones del álgebra y los grupos de Lie, un párrafo acerca de las aplicaciones en robótica que tiene la rotación de matrices homogéneas y sus grafos que interpretan estos objetos. Técnicas que permiten desarrollar aplicaciones que sustentarán el autómata.
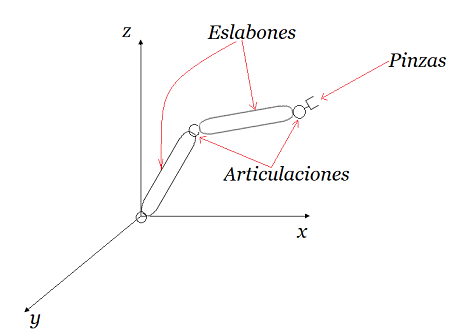
Diag#1: Rotación Matrices Homogéneas en $R^3$
El robot del diagrama $Diag\text{#}1$, es un conjunto de tres cuerpos rígidos, dos eslabones y una pinza.
Dotado de articulaciones que permiten movimientos rotatorios entre sus partes.
Este sistema de cuerpos rígidos articulados ($Diag\text{#}1$), es posible representarlo mediante un grafo $G$.
Es decir, realizar una abstracción desde la Teoría de Grafos con puntos y líneas. $[B57]$
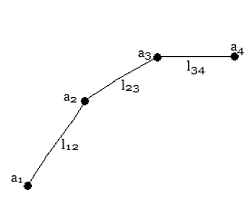
Grafo Asociado a $Diag\text{#}1$
|
$$M=\begin{pmatrix} \text{ } & \mathbf{a_{1}} & \mathbf{a_{2}} & \mathbf{a_{3}} & \mathbf{a_{4}} \\
\mathbf{ a_{1}} & 0 & 1 & 0 & 0 \\
\mathbf{a_{2}} & 1 & 0 & 1 & 0 \\
\mathbf{a_{3}} & 0 & 1 & 0 & 1 \\
\mathbf{a_{4}} & 0 & 0 & 1 & 0 \\
\end{pmatrix}$$
Matriz Adjunta
|
Su grafo $G$ asociado consiste de cuatro puntos $V=\unicode{123} a_1,a_2,a_3,a_4 \unicode{125}$, donde cada par de puntos está unido por una línea. Llamemos $L=\unicode{123} l_{12},l_{23},l_{34}\unicode{125}$, las líneas vinculadas a sus puntos adyacentes, i.e. cada línea rotulada de acuerdo a sus subíndices incide en cada punto. Se dice que $G$ es un grafo $a(4,3)$ conexo. (Nótese que el número de líneas es igual al número de puntos menos $1$, $q=p-1$)
Los elementos de la matriz adjunta $M$ señalan con el valor $1$ cuando existe adyacencia entre los puntos y con valor $0$ cuando no la hay. Nótese que $G$ es un grafo no direccionado.
Adicionalmente, las líneas o arcos o aristas pueden ser direccionados. Este tipo de grafos se denominan también dígrafos o grafos cinemáticos y a los puntos se les denomina vértices. Las matrices que representan un dígrafo son de incidencia asimétrica.
A continuación se ilustra el dígrafo o grafo el direccionado $G^*$ y su matriz $G^*$ asociada:
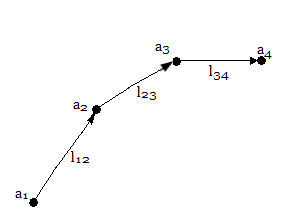
Dígrafo Asociado a $Diag\text{#}1$
|
$$M^*=\begin{pmatrix} \text{ } & \mathbf{a_{1}} & \mathbf{a_{2}} & \mathbf{a_{3}} & \mathbf{a_{4}} \\
\mathbf{ a_{1}} & 0 & 1 & 0 & 0 \\
\mathbf{a_{2}} & 0 & 0 & 1 & 0 \\
\mathbf{a_{3}} & 0 & 0 & 0 & 1 \\
\mathbf{a_{4}} & 0 & 0 & 0 & 0 \\
\end{pmatrix}$$
Matriz Adjunta Dígrafo
|
A partir, de estos datos básicos de adyacencia se pueden configurar un conjunto de matrices que describen y controlan los movimientos del robot, mediante los algoritmos de computación que gestionan el sistema sensorial del robot.
Un par de nodos rotatorios o articulaciones cinemáticas acopladas a los eslabones (líneas) del robot de la figura $Diag\text{#}1$, permiten un movimiento relativo entre ellos, de modo que este movimiento puede ser interpretado y descrito por el software que controla al robot, leyendo la data desde las matrices en $R^n$.
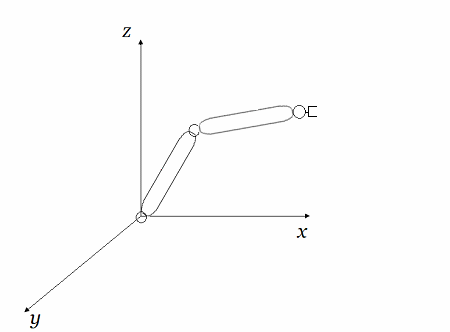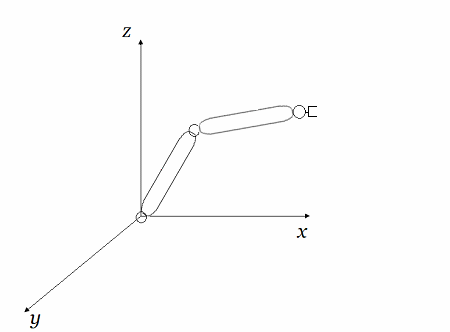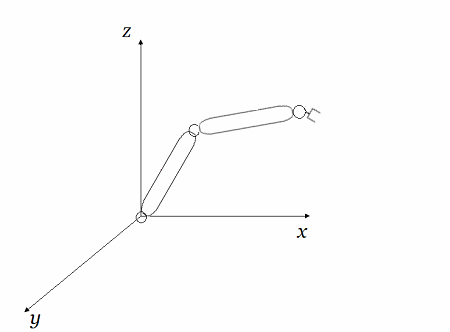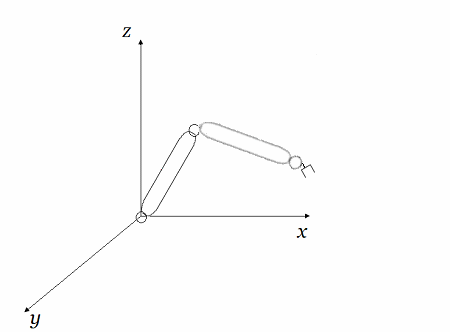
Diag#2: Rotación Articulaciones $a_3$ (Pinza $l_{34}$) y $a_2$ (Eslabón $l_{23}$) en $R^3$
Matriz basada primero en la adyacencia y posteriormente con matrices representativas que contienen más información rotatoria localizada en las celdas, donde existe relación, tanto con componentes subordinación, de jerarquía o de otras características de control.
Resumiendo, diremos que un grafo $G(V,L)$ es el conjunto de todos los vértices y todas la líneas o arcos, donde surge
una propiedad isomorfismo de grupos de $G$ con la matriz de adyacencia y también a la matriz de incidencia.
Se puede visualizar el diagrama, su grafo asociado y sus matrices, que existe simetría entre esos objetos matemáticos, i.e. son invariantes bajo la acción de esas transformaciones dotadas de una inversa.
$$
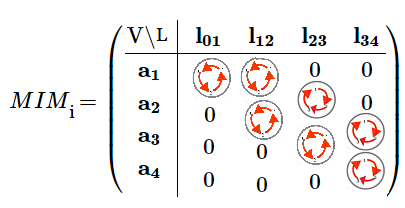
MIM_n=\begin{pmatrix} \text{V\L} & \mathbf {l_{01}} & \mathbf {l_{12}} & \mathbf {l_{23}} & \mathbf {
l_{34}} \\
\mathbf{a_{1}} & 1 & -1 & 0 & 0 \\
\mathbf{a_{2}} & 0 & -1 & 1 & 0 \\
\mathbf{a_{3}} & 0 & 0 & -1 & 1 \\
\mathbf{a_{4}} & 0 & 0 & 0 & 1 \\
\end{pmatrix}
$$
Para terminar este párrafo introductorio, se esboza una explicación del paso desde esta matriz de incidencia modificada (MIM) hacia un grupo de lie, donde cada entrada se transforma desde un escalar a una matriz, sustituyendo los $1$ por la matriz idéntica o unidad $I$ y los valores $0$ por la matriz nula.
Puesto que el movimiento relativo entre dos eslabones (líneas) puede ser descrito por un giro de las articulaciones, i.e. todo movimiento relativo en el espacio del conjunto de elementos (figura $Diag\text{#}1$), es una combinación lineal de estos objetos que son linealmente independientes. A partir ahí, se construye un subespacio con restricciones de control para todos los posibles movimentos del robot. (Ver Obtencion del Modelo Dinámico Simbólico de Robots Ramificados Utilizando Grupos de Lie y Grafos  , Universidad Carlos III de Madrid, 2016). , Universidad Carlos III de Madrid, 2016).
Nótese que el proceso de transitar desde el brazo robótico de la figura ($Diag\text{#}1$), mediante grafos asociados, matrices, rotación y permutaciones, tiene por objeto reducir y obtener representaciones isomorfas con grupos de Lie, sobre los cuales se tiene información y es posible tabular la data, utilizando grupos de permutaciones y matrices.143
Más adelante se puede agregar un conjunto de matrices de estado, donde sus articulaciones puede ir variando entre una rotación par (+1), impar (-1), o cero, de acuerdo al control paramétrico que asignado. (Ver Generadores SO(3) en el artículo Definición Algebra de Lie).
De igual forma un robot puede ejecutar distintas funciones computacionales, a fin de generar códigos o emitir informes estadísticos o automatizar procesos de otra índole (Ver artículo RobotDocIRS, Video: Experimento ~ Supervisión y Entrenamiento ~ Inteligencia Artificial ~ Naïve Bayes ~ Learning Machine).
La introducción cada día más creciente del Algebra de Lie en el desarrollo de la robótica, ciertamente está logrando
estimaciones con más precisión, consistencia y estabilidad en los diseños de múltiples rotaciones que involucran superficies topológicas lisas de los grupos de Lie([B56]). Esto se manifiesta en el trabajo sobre variedades de rotación $SO(3)$106 y los enfoques de mapeo exponencial (Ver Video Grupo de Lie - Enfoque Exponencial).
Pauli - Algebra de Lie - Robótica
Representaciones y Learning Machine
Así mismo, otros conjuntos de matrices de grupos de Lie que están disponibles para aplicaciones prácticas en diversos ámbitos. Por ejemplo, en el aprendizaje automático "Learning Machine", que es una rama de la inteligencia artificial, que cada día más juega un rol creciente en la investigación científica.
En efecto, el Algebra de Lie proporciona, por un lado representaciones geométricas de datos, y por otro lado soluciones algebraicas específicas. Es decir, es posible asociar grupos de Lie a estas representaciones geométricas, mediante un concepto topológico y Teoría de Grafos
[B57]
Las representaciones geométricas que generan los datos dentro de un contexto, - sobre el cual se tiene conocimiento y experiencia -, es posible establecer relaciones entre causa y efecto, con evidencias y resultados, entre la data de entrada y de salida.
El proceso intermedio entre Entrada y Salida, generalmente ocurre con minería de datos, donde se estructura, analiza y formulan determinadas reglas sobre las cantidades masivas de datos de Entrada sin procesar. En la práctica, a estos datos se les aplican unos ciertos criterios de búsquedas, con el propósito de encontrar patrones y errores, a través de algoritmos matemáticos, computacionales y técnicas de minería de datos, que filtran, limpian, ordenan y validan los resultados de Salida.
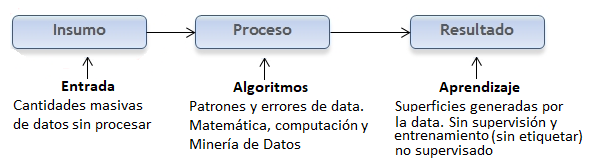
Datos: Entrada $\rightarrow$ Proceso $\rightarrow$ Salida
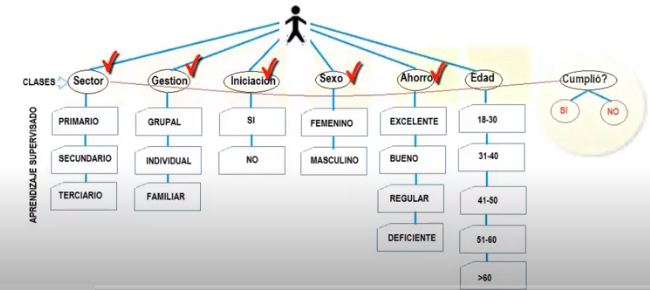
Clasificación Modelo ~ Naïve Bayes
En general, se trata de modelos predictivos, los cuales permiten pronosticar o responder preguntas. Las respuestas se expresan en clases, sean binarias o de atributos clasificados. Es decir, se predice información en base a datos numéricos agregados en clases y transformarse en herramientas de aprendizaje automático e inteligencia artificial. (Ver Naïve Bayes ~ Simple Algoritmo de Clasificación Modelo de Variables Discretas y Experimento ~ Supervisión y Entrenamiento ~ Inteligencia Artificial ~ Naïve Bayes Learning Machine)
- Espacio de Aprendizaje ~ Diagrama de Dynkin
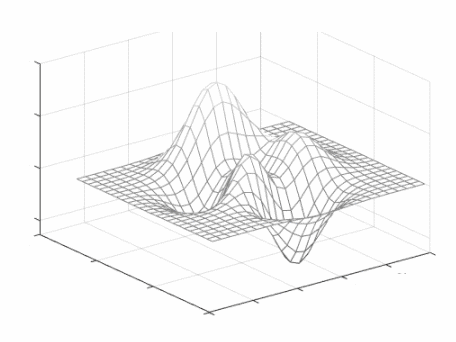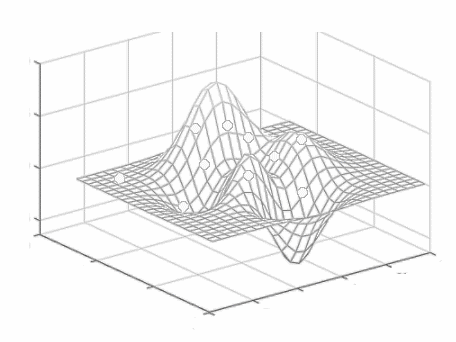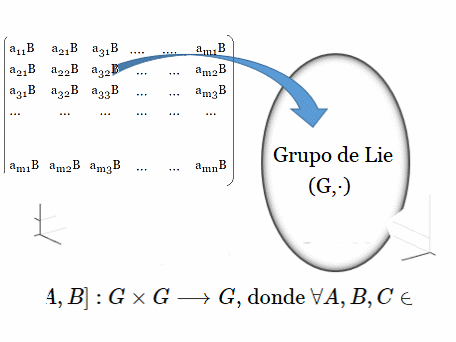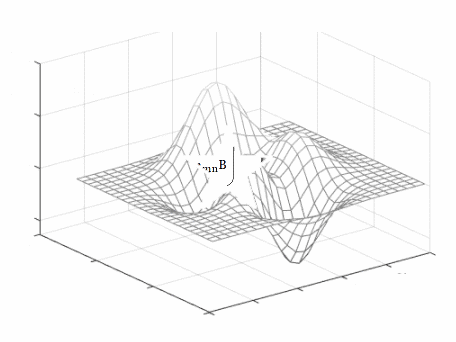
Data$\rightarrow$Superficie$\rightarrow$Grafo$\rightarrow$Matriz Asociada$\rightarrow$Grupo de Lie
Entonces, con las frecuencias relativas que generan estas enormes cantidades de datos (con o sin supervisión y entrenamiento), se ajusta una superficie que permite desarrollar algoritmos con una predicción bayesiana de la salida para las próximas entradas.
Estas superficies generadas por la data, - sin supervisión y entrenamiento (sin etiquetar) -, pueden lograr que el sistema modele la estructura inherente de esos datos con precisión. Es decir, el aprendizaje no supervisado es útil en los casos en que el desafío es descubrir y configurar un algoritmo, con las implícitas relaciones en un conjunto de datos sin estructurar.
Efectivamente, desde el análisis de datos se examina un conjunto enorme de registros capturados, con el propósito de sacar conclusiones y patrones, con los cuales es posible transformar la data en información.
Es decir, para descubrir o ampliar conocimientos, sea por la experiencia que sustentan algunas hipótesis predeterminadas o para establecer nuevos patrones de comportamiento desde la muestra de datos analizada.
La recolección de datos puede revelar clasificaciones que ayudan a confirmar o descartar supuestos acerca de los modelos existentes.
En el caso de que el algoritmo muestre que el problema de aprendizaje se puede resolver, entonces se recurre a diagramar un espacio de aprendizaje (Diagrama de Dynkin113), conformado por los datos y su correspondiente Grupo de Lie.

André Henriques - Lie algebras and their representations
Para aquellos que requieran profundizar sobre las representaciones de Dynkin y Algebra de Lie, recomiendo ver la clase de "Lie Algebra Representations" del profesor André Henriques  (Instituto de Matemáticas de la Universidad de Oxford) publicada en Youtube en agosto del 2015. (Instituto de Matemáticas de la Universidad de Oxford) publicada en Youtube en agosto del 2015.
En otras palabras, se puede configurar un algoritmo de aprendizaje geométrico con los Grafos Dynkin
en Lie group Machine Learning (LML). Mediante este algoritmo se visualiza si el problema de aprendizaje tiene solución. De modo que una vez resuelto, con el Diagrama de Dynkin se configura desde ese espacio de aprendizaje. El diagrama es un grafo asociado con su matriz adjunta que se modeló, a partir de los datos que generaron la superficie.115.
Luego, de acuerdo con ese Diagrama de Dynkin esbozado por la data recolectada, se encuentra un grupo de Lie asociado con su solución correspondiente. Por tanto, el grupo de Lie es una herramienta de base para la teoría del aprendizaje automático.
Estas son solo algunas formas de mostrar gráficamente las representaciones de los generadores de Lie, y la elección gráfica adecuada dependerá del contexto específico y la dimensión de la representación.
Un Diagrama de Dynkin es una herramienta utilizada en la teoría del Algebra de Lie, la geometría algebraica y la teoría de grupos para representar de manera visual la estructura de un grupo de Lie. Estos diagramas son especialmente útiles para clasificar. (Ver Video Variedad Diferenciable - Definición Algebra de Lie)
Los diagramas de los generadores de Lie, como los del grupo $ \text{SL}(2,\mathbb{C}) $, pueden ser expresadas gráficamente de varias formas, dependiendo del contexto y la dimensión de la interpretación. Por ejemplo, para representaciones de Grupo $\mathbf {Sl_2 \longrightarrow}$ Algebra de Lie $\mathfrak{\Large g}$ de dimensión finita, como las representaciones fundamentales, se pueden tratar como espacios vectoriales tridimensionales.
Los diagramas de Dynkin son una forma común de visualizar los álgebras de Lie simples y sus representaciones. En el caso de $ \text{SL}(2,\mathbb{C}) $, el álgebra de Lie correspondiente es $ \text{su}(2) $, donde es posible visualizar gráficamente sus generadores de la Algebra de Lie con Dynkin.
Es importante tener en cuenta que para grupos de Lie más complicados, los Diagramas de Dynkin pueden ser mucho más grandes y complejos, pero este ejemplo simple ilustra los conceptos básicos detrás de ellos.
- Software de Reconocimiento Facial
Por ejemplo, este mismo concepto del Diagrama de Dynkin se utiliza en los softwares de reconocimiento facial de un individuo. Ver video de National Geographic El Verdadero Tutankamón (Minuto 12:15)  , donde en un segmento del video se muestra el método e investigación del profesor Amit Roy-Chowdhury, de la Universidad de California en Riverside (UCR), Estados Unidos. , donde en un segmento del video se muestra el método e investigación del profesor Amit Roy-Chowdhury, de la Universidad de California en Riverside (UCR), Estados Unidos.
En ese segmento del video se explica el procedimiento del algoritmo, que es resumidamente lo siguiente:
Se crea una malla en la superficie de un rostro y se marcan los puntos de interés como los anillos de los ojos, la nariz, los pómulos y la boca. Es decir, se van identificando, localizando y mapeando los rasgos faciales, hasta alinear la malla con la cara de la persona.
Desde ahí, el algoritmo determina un número finito de puntos de referencias, generando un grafo asociado con un patrón único de la cara.
El algoritmo, ciertamente está montado sobre robustas bases de datos, dotado de un modelo de Learning Machine con atributos de clasificación, observaciones estadísticas iteradas, métricas, supervisión y entrenamiento.
Cierre de Formalización
Mencionado lo anterior acerca de ciertas aplicaciones del Algebra de Lie, volvemos al centro del presente artículo, donde nos enfocamos a partir de las Matrices de Pauli y los espacios vectoriales unitarios isométricos, i.e. conservan la métrica o norma, dotados de la operación binaria producto interno, con matrices cuadradas $M_{n \times 2}$, cuya determinante $det(M) \ne 0$ y son ortogonales $M·M^{T}=M^{T}·M$. Estos conjuntos de matrices que operan bajo la multiplicación de matrices se conocen como especiales, ortogonales de dimensión $n$, $G=\unicode{123} M \in SO(n) \text{/} det(M)=1 \land M^{T}M=M^{T}M=I\unicode{125}$. (Ver Video I. Grupo de Lie ~ Enfoque Geométrico ~ Matrices de Pauli y Algebra de Lie)
En los videos asociados (Enfoques Exponencial e Infinitesimal), se trata y describe la aplicación exponencial de un Grupo de Lie que permite establecer correspondencia entre el Algebra de Lie y el Grupo de Lie.
Espacio Vectorial de las Matrices de Orden $n×n$
Sea $Mn(K)$ el espacio vectorial de las matrices de orden $n×n$ sobre un cuerpo $K$. Donde
esta estructura vectorial, se define con la operación ordinaria de multiplicación. Entonces cumple con las siguientes propiedades básicas:
Si $A,B,C \in Mn(K)$, entonces:
- Distributiva: $A(B + C) = AB + AC,\quad (A + B)C = AC + BC$
- Asociativa: $A(BC) = (AB)C$
- En general, $AB\ne BA$
- La matriz identidad verifica: $AI = IA = A$
En el presente caso, he trabajado con matrices ortogonales sobre el espacio n-dimensional donde el cuerpo K en este documento siempre lo consideramos como los Reales o Complejos.
$SO(n)\longrightarrow \mathbf {\mathit{so(n)}}$
106
Es decir, conmutan los elementos, - que son matrices-, en un espacio de dimensión $n$, sobre un campo $K$
Corchetes de Lie ~ Levi-Civita
Utilizando el símbolo Levi-Civita107 en dos dimensiones, donde $+1$(par) representa la rotación en el sentido de los punteros del reloj y $-1$(impar) contrario al sentido de los punteros del reloj:
$$
\epsilon _{ij} =
\begin{cases}
+1, & \text{si (ij) es (1,2)} \\\\
-1, & \text{si (ij) es (2,1)}
\end{cases}
$$
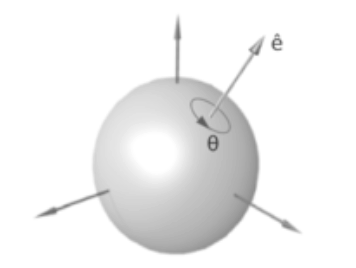
$SO(3)$:Rotación Tridimensional
Ahora, en $SO(3)$,- i.e. en tres dimensiones-, los elementos generadores infinitesimales $\unicode{123}X_1,X_2,X_3\unicode{125}$ y sus relaciones de conmutación constituyen un Algebra de Lie:
$$X_1=\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}$$
$$X_2=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{pmatrix}$$
$$X_3=\begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$$
Aquí comprobamos que:
$$[X_1,X_2]=X_3,\qquad [X_2,X_3]=X_1,\qquad [X_3,X_1]=X_2$$
Si se aplica la operación Corchetes de Lie, por ejemplo $[X1,X2]=X_1·X_2-X2·X_1$ operando con las matrices, se tiene:
| $$X1X2$$
| $$-$$
| $$X2X1$$
| $$=$$
| $$X3$$
|
| $$\downarrow$$ |
|
$$\downarrow$$ |
|
$$\downarrow$$ |
| $$\begin{pmatrix} 0 & 0 & 0 \\ 1& 0& 0 \\ 0 & 0 & 0 \end{pmatrix}$$ |
$$-$$ |
$$\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$$ |
$$=$$ |
$$\begin{pmatrix} 0 & -1 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}$$ |
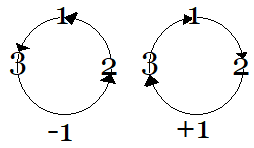
Rotación impar(-1) y par(+1) Dimensión 3
A fin de simplificar las operaciones de permutación, se recurre a la utilización del símbolo Levi-Civita en tres dimensiones:
$$
\epsilon _{ijk} =
\begin{cases}
+1, & \text{si (ijk) es (1,2,3)(2,3,1)(3,1,2)} \\\\
-1, & \text{si (ijk) es (3,2,1)(2,1,3)(1,2,3)} \\\\
\text{ }0, & \text{si (ijk) ~ i=j o j=k o k=i}
\end{cases}
$$
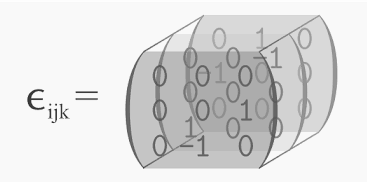
Matriz Dimensión 3 con Símbolo de Levi-Civita107
Es decir, en vez de multiplicar explícitamente las matrices generadoras de $3\times 3$, sintetizamos con los indicadores del símbolo de Levi-Civita, donde $\epsilon=1$ si es una permutación par(+1), $\epsilon=-1$ si es una permutación impar(-1) y $\epsilon=0$ en cualquier otro caso. Por ejemplo, ilustremos tres casos:
| $$[X_2,X_3]=\\
\epsilon_{231}X_1=X_1\\
\require{cancel}\cancelto{0}{\epsilon_{232}}X_2=0\\
\require{cancel}\cancelto{0}{\epsilon_{233}}X_3=0\\
$$ |
$$[X_1,X_2]=\\
\require{cancel}\cancelto{0}{\epsilon_{121}}X_1=0\\
\require{cancel}\cancelto{0}{\epsilon_{122}}X_2=0\\
\epsilon_{123}X_3=X_3\\
$$
|
$$[X_2,X_1]=\\
\require{cancel}\cancelto{0}{\epsilon_{211}}X_1=0\\
\require{cancel}\cancelto{0}{\epsilon_{212}}X_2=0\\
\epsilon_{213}X_3=-X_3\\
$$
|
Por tanto, de esa forma se puede representar todas la permutaciones tridimensionales del Algebra de Lie, desde $SO(3)$.
Una excelente ilustración es el Cubo de Rubik, cuya imagen animada se muestra a continuación, dado que es un ejemplo de un grupo de permutación. Los grupos de simetría $SO(n)$ son grupos de permutación, donde cada una de las rotaciones, en este caso con alguna de las caras del Cubo de Rubik-, constituye una permutación. Estas rotaciones forman un conjunto generador del Algebra de Lie.
Definición Algebra de Lie 
 Video: Definición Algebra de Lie Video: Definición Algebra de Lie
Continuación$\longrightarrow$
Ver artículo complementario Grupo de Lie - Enfoques Geométrico y Exponencial 
Ver Video: Grupo de Lie ~ Complementario a Matrices de Pauli y Algebra de Lie 
|




 Video Definición Algebra de Lie
Video Definición Algebra de Lie





















 (Instituto de Matemáticas de la Universidad de Oxford) publicada en Youtube en agosto del 2015.
(Instituto de Matemáticas de la Universidad de Oxford) publicada en Youtube en agosto del 2015.
