|
Grupo de Lie102 |
|
v.4.1/Junio 2021 |

|
 Grupo de Lie ~
Enfoque Geométrico Grupo de Lie ~
Enfoque Geométrico |
| + Ficha Técnica |
| + Mapa Publicaciones |
| + Videos Asociados |
| + Conceptos Claves |
|
Algebra de Lie ~ Variedades114 Diferenciables
|
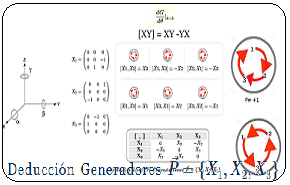
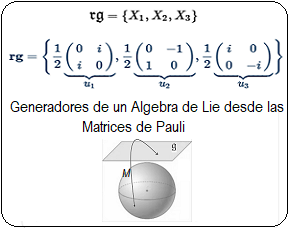
El presente artículo, - que proviene de la publicación Matrices de Pauli y Algebra de Lie
89,
consta de dos partes I y II, en el medio un desarrollo algebraico que describe la transición mediante cálculo diferencial entre ambas partes:
Los tres enfoques convergen a la deducción de la matriz real $M_{2\times 2}$, - sobre un ángulo de rotación $\alpha$ en torno a un origen o centro de rotación -, que constituye un Grupo de Lie:
El segundo enfoque Matriz Exponencial, deduce la matriz $M$ desde la constante universal $e ^{A}$, i.e. con exponente matricial, desarrollado con series de Taylor hasta su demostración.
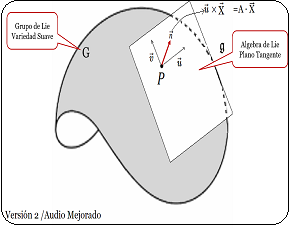
Los Grupos de Lie aquí tratados son continuos de dimensión infinita o grupos continuos de simetría con una estructura de variedad diferenciable81.
Estas matrices de rotación pasiva son cuadradas, pueden ser de tamaño $n\times n$ y son ortogonales. Sus elementos de entradas son números reales. Su característica central es que su determinante es igual a uno. Esto implica que la matriz opera girando el sistema de referencia sobre un vector, donde esta magnitud física permanece invariante. Estas matrices se utilizan en los operadores más comunes de la computación cuántica96 y constituyen el grupo especial ortogonal o Special Orthogonal $SO(n)$.
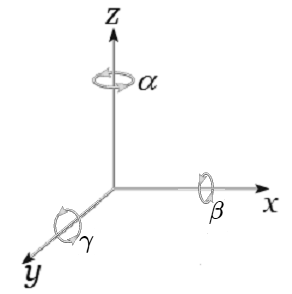 Figura 1:Rotacion Pasiva sobre el Plano XYZ
Dicho esto, damos comienzo a esta sección anexa y compacta acerca del Grupo de Lie
en el espacio euclidiano real $\mathbb R$, cuyos
orígenes textos, imágenes, animaciones, etc. fueron extraídas del documento Matrices de Pauli y Algebra de Lie y su correspondiente síntesis publicada en el video en YouTube del mismo nombre, donde se describe con más detalles que un grupo de rotación en torno a un punto fijo, que constituye un Grupo de Lie. Este concepto se entiende como una transformación del sistema de coordenadas bajo el espacio vectorial de Hilbert3, con sus bases ortonormales.
A su vez, la base de ese documento es el
trabajo central Conceptos Matemáticos Básicos de
Computación Cuántica 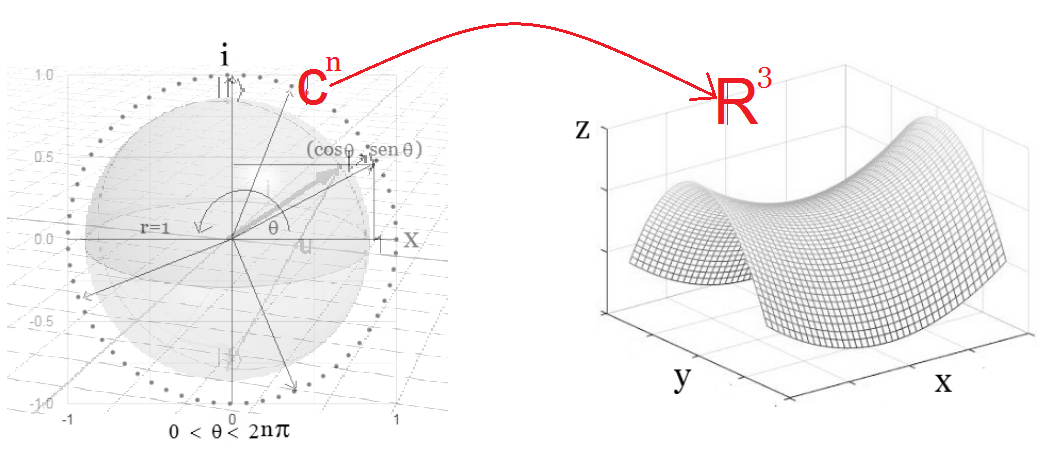
Figura 2: Transformación $\mathbb C\longrightarrow \mathbb R$
A continuación, intentaré mostrar que la matriz $M_{2\times 2}$, definida en los reales como se indica en $[L1]$,
es un Grupo de Lie de rotación ortogonal especial de dimensión $2$, $SO(2)$.
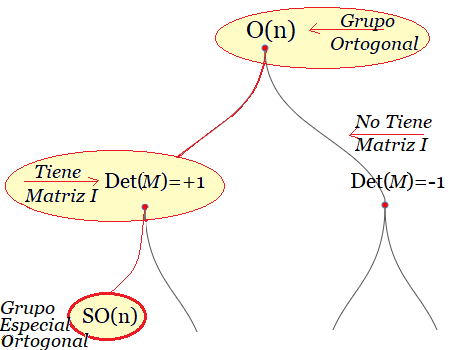 Clasificación Grupos SO(n)
Es decir, $G$ es el conjunto de todas las matrices de $M_{2\times 2}$ ortogonales que pertenecen al 'Special Ortogonal of order 2' del espacio euclídeo tridimensional (Esfera de Bloch) con determinante igual la unidad.
Incluir esta explicación complementaria y anexa a la exposición de Matrices de Pauli y Algebra de Lie, tiene cierta importancia didáctica, dado que es un enfoque geométrico en el plano utilizando trigonometría. 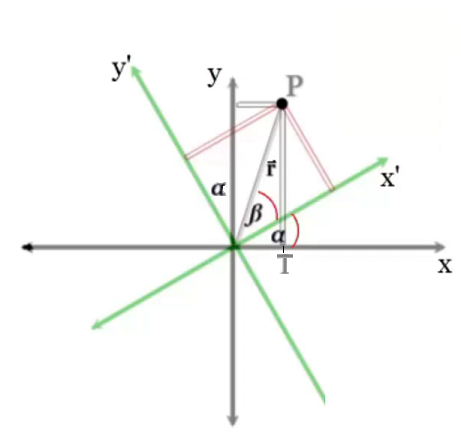
Figura 3: Diagrama Base Deducción $M$ (Ver Desarrollo Deducción)
Y con esa base se allana el camino
para extenderse a grupos de Lie con
matrices de dimensión $n \times n$, como
asimismo con valores infinitesimales y
límites (Ver más adelante $M_{n \times n}$).
Estamos interesados en la operación
central que ejecuta una rotación de un
vector $\overrightarrow{OP}$,
en el plano $XY$. Justamente al aplicar
este operador matricial $M$ sobre un
ángulo $\alpha$ se obtiene un vector girado
$X'Y'$, pero el giro es desde el punto de vista del observador no del vector propiamente tal.
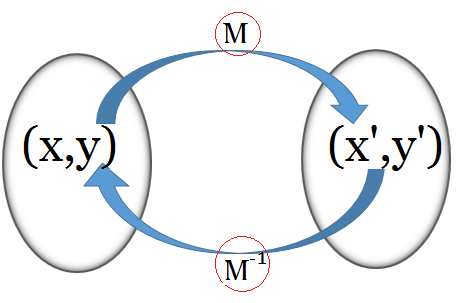
Figura 4: Transformación $MX=X'$
Lo interesante es que la simple matriz $M$
conformada por las funciones
trigonométricas básicas senos y cosenos,
genera una rotación del plano, donde gira
el sistema de coordenadas con invariabilidad de la métrica.
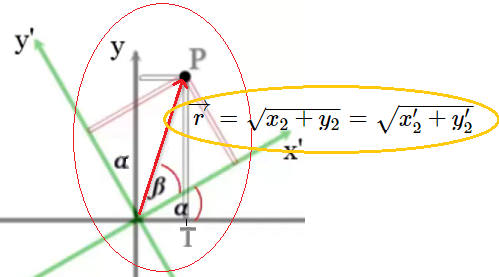
Figura 5: $\overrightarrow r$ Invariante
En otras palabras, la operación de
rotación no alarga ni acorta el objeto
y lo transforma en una variedad real. Es
decir, en un grupo diferenciable
infinito y continuo.
Detrás de esa extensión, está la rotación de un vector $\overrightarrow{OP}$ conserva las propiedades principales hacia una clase de conjuntos más amplia compuesta por una clase infinita de uniones de elementos. 
Figura 6: Rotación del Plano ~ Preserva $\overrightarrow r$
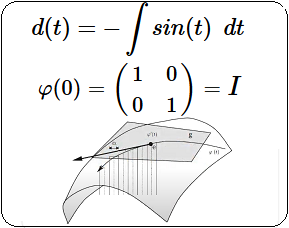
$$\lim_{\alpha\to 0}M(\alpha)=I\\
x'=r·cos(\alpha + d\alpha)\\
y'=r·sin(\alpha + d\alpha)
$$
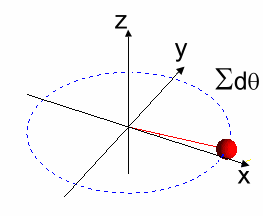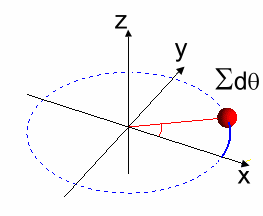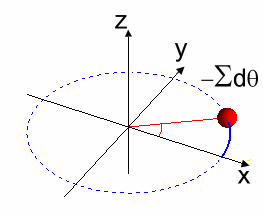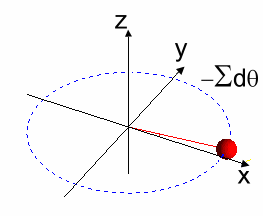
Figura 7: Rotación por Segmentos Infinitesimales $d\alpha$
Esto explica que existe
un neutro, - que es la matriz identidad $I$ -, y
que para cada elemento existe un inverso.120.
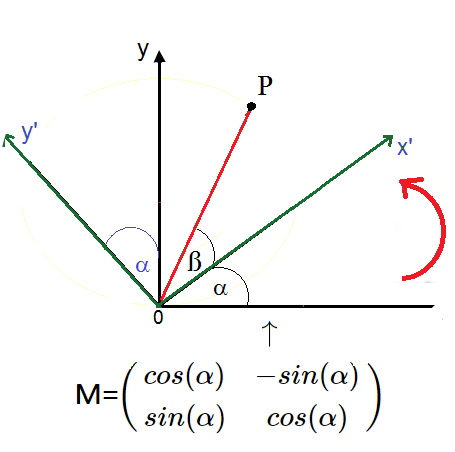
Figura 8: Diagrama Geométrico $\longrightarrow M$
Vamos a deducir, - desde la figura 2 -,
aplicando trigonometría,
cómo se estructura la transformación lineal
$M$, compuesta simplemente por los
elementos senos y cosenos.
ii) Su transpuesta es igual a la inversa, esto implica que: iii) $M$ es ortogonal, dado que una matriz ortogonal es una matriz real, cuya inversa es igual a su transposición. iv) La transformación $M$ preserva invariante la métrica con su magnitud física de $\overrightarrow r$, el radio del origen al punto $P$.
Es decir, la magnitud física de $\overrightarrow r$ es la misma, tanto en el plano $XY$ como en el
en el plano $X'Y'$.
Ahora, calculemos estas
características i), ii), iii) y describamos iv),
que hemos señalado para la matriz $M$.
Es decir, $Det(M)=1$ demostrándose el punto i).
Esta matriz es la transpuesta, vamos a multiplicar
directamente la transpuesta $M^{T}$ por la
matriz $M$ y si nos da la Identidad implica que $M^{T}$
es la Inversa.
Entonces, multiplicando $M^{T}M$ resulta la matriz identidad.
Esto implica que la transpuesta $M^{T}$ es la
matriz inversa. De modo que tanto sus productos son
igual a la matriz identidad.
Un Grupo de Lie con esta caracterización,
puede concebirse físicamente como un
conjunto de transformaciones infinitesimales. Es decir, infinito y continuo
cuyas rotaciones se dan sobre el espacio
euclídeo, representadas por el conjunto
de matrices ortogonales de $2\times 2$ y con
determinante igual a la unidad.
A continuación, deduciremos
Geométricamente la matriz $M$, desde el
diagrama que ilustra la rotación $\mathbf {\alpha}$
utilizando funciones trigonométricas.
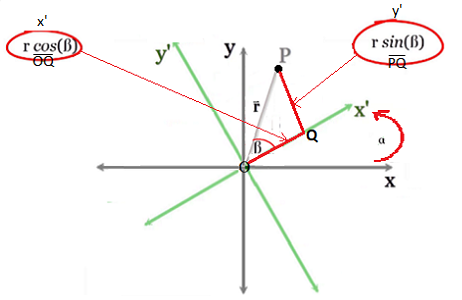
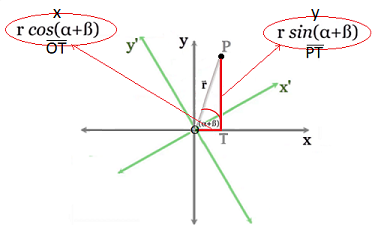
Luego, sobre el plano $XY$ se observa el
triángulo $OPT$, desde su ángulo compuesto $(\alpha + \beta)$,
se proyecta el cateto adyacente con las coordenadas $x$ igual a $r·cos(\alpha + \beta)$
la del cateto opuesto y igual $sin(\alpha + \beta)$.
A este último sistema de coordenadas, le
aplicamos una fórmula de las identidades
trigonométricas fundamentales del coseno
y seno sobre la suma de dos ángulos, y
obtenemos las siguientes dos expresiones:
Donde se desagregan el seno y el coseno
en forma individual en función de los
ángulos $\alpha$ y $\beta$
Entonces comenzaremos a utilizar las descripciones tanto $x'$ como $y'$ y las vamos a ir sustituyendo de la siguiente manera: 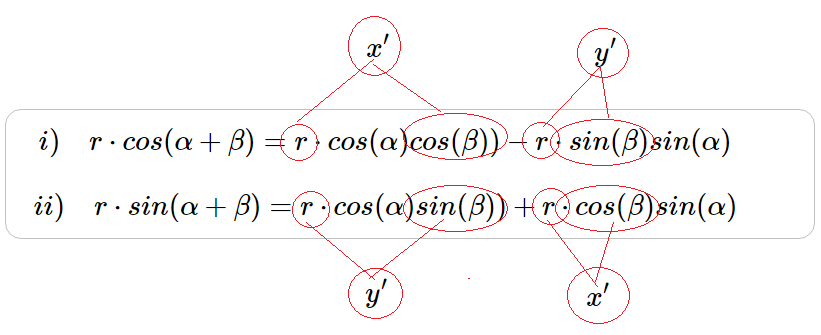
Figura 10: Sustitución de $x', y'$
Se obtuvo la sustitución en función de $\alpha$, en tanto $x'=r·cos(\beta)$ y $y'=r·sin(\beta)$. De donde se configura el siguiente sistema de ecuaciones lineales:
Luego ponemos estas ecuaciones en forma
matricial. De donde surge la matriz $M$,
la cual es la transformación del plano $XY$
hacia el plano $X'Y'$, como lo
vimos en la caracterización,
en la sección anterior.
Así mismo, utilizando la expresión $[L2]$ se ilustra la transformación inversa $M^{-1}=M^{T}$:
De esa manera utilizando la geometría
sobre el plano euclidiano, hemos
deducido la matriz $M$, cuya
caracterización demuestra que es un
Grupo de Lie $SO(2)$. Es decir, del grupo
especial ortogonal de dimensión dos, de la forma:
|
|
El objetivo de lo descrito en los párrafos previos ha sido enfocar un Grupo de Lie como un objeto geométrico con una forma dibujable y didáctica, aunque los Grupos de Lie del álgebra abstracta no es siempre posible visualizarlos como en los ejemplos anteriores.
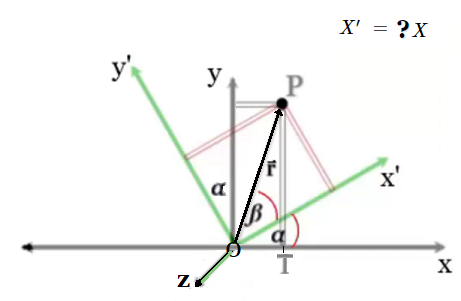 Figura 3: Matriz en $\mathbb R^3$ que Genera una Rotación Pasiva
En otros términos, se aplica el mismo procedimiento previo de $SO(2)$, i.e. una matriz aumentada $M_{3 \times 3}$ que multiplicada por el vector $X$ obtenga estas nuevas coordenadas en $X'$:
Este conjunto de matrices cumple las condiciones de rotación en el plano euclidiano y constituye un Grupo de Lie en $SO(3)$.
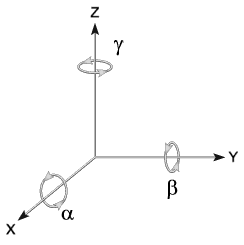 Figura 3.1: Rotaciones Independientes en Torno a Ejes 121
En el espacio $\mathbb R^3$ se especificará la matriz que gira un vector por un ángulo alrededor de un eje del espacio tridimensional. Se utilizarán las matrices fundamentales, las cuales son rotaciones que determinan cada par de ejes ortogonales.
Las rotaciones se realizan sobre los ejes de coordenadas Cartesianas en el espacio tridimensional euclidiano, se identifican los ángulos de rotación en torno a cada eje, tomando como referencia el giro en torno al eje $z$ como $\gamma$, el giro en torno al eje $y$ como $\beta$, y el giro en torno al eje $x$ como $\alpha$.
Las transpuestas de las matrices son sus respectivas inversas. Es decir, son ortogonales:
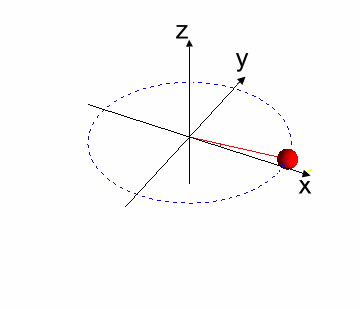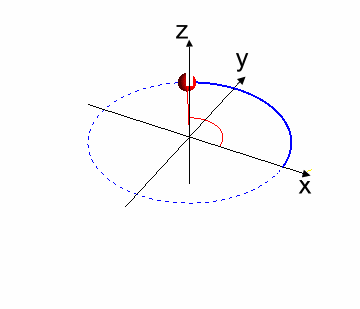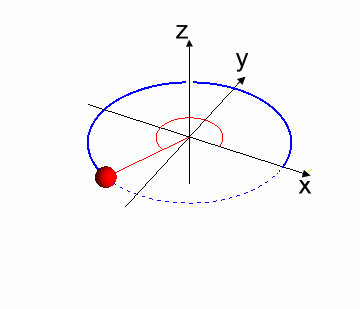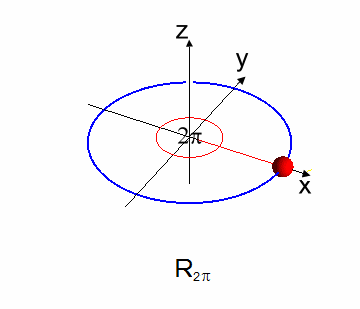 $SO(2)$ Impar en $\mathbb R^3$ por Tramos de $\frac{\pi}{4}$
En caso de tener que trabajar con matrices complejas, i.e. matrices unitarias que contengan números imaginarios (dentro de los espacios de Hilbert), entonces la ortogonalidad se muestra mediante la igualdad de la transpuesta de su conjugado complejo, también denominada "daga" de la matriz y denotada con el símbolo +.
- Matriz de Rotación $M \in SO(n)$
 $$ \text{, donde } m_{ij}\in \mathbb {R} $$
Donde la matriz $M_{n\times n}$ tiene la misma caracterización que se determinó para $M_{2\times 2}$, i.e:
Por tanto, $\Rightarrow M^{T}M=M^{T}M=I$, de donde la ortogonalidad de $M$ explica la métrica invariante. De modo que $S^{2}=X^{T}X=(X')^{T}X$ 94
La métrica invariante es $S^{2}=XX^{T}=X'(X')^{T}$:
Por tanto, que la transpuesta de una matriz real cuadrada $n \times n$ sea igual a su inversa, i.e. $M^{T}=M^{-1}$ y que la magnitud del vector permanezca invariante bajo una rotación de las coordenadas, implica directamente que $M$ es ortogonal.
|
|
Introducción Enfoque Infinitesimal~Taylor
Retomemos la matriz $M(\alpha)_{2\times 2}$, que se definió en $[L1]$, haciendo un cambio de notación y designando la transformación como $R(\theta)$, a fin de utilizar u homologar la notación de los enfoques de rotación infinitesimal más comunes abordados en la Matemática-Física 99 .
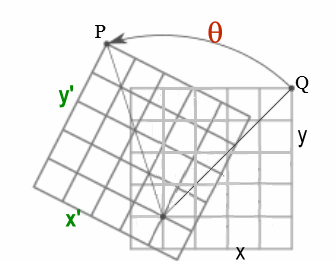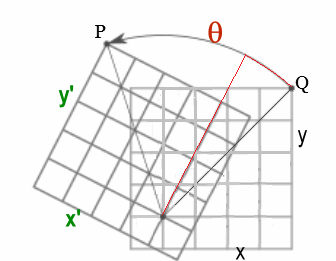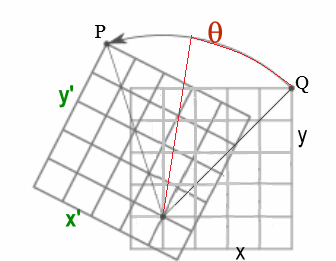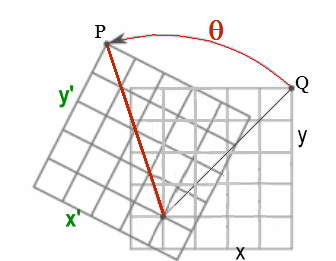 Rotación Plano ~ Cambio Sistema Coordenadas
La matriz $R(\theta)$ produce la misma rotación pasiva de un ángulo $\alpha$ sobre el sistema de coordenadas cartesianas visto previamente y constituye un Grupo de Lie de la forma:
De las características de esta matriz (Ver $[L3]$), tenemos que $M^{T} \times M^{-1} = M^{-1}M^{T} =I$. Esta propiedad simplemente admite aplicar la ley de composición:100 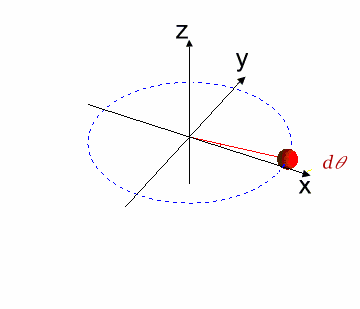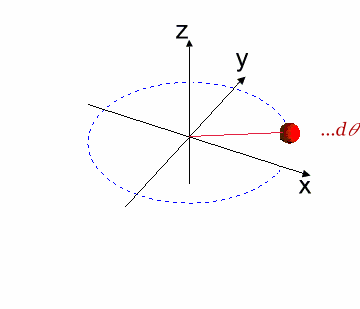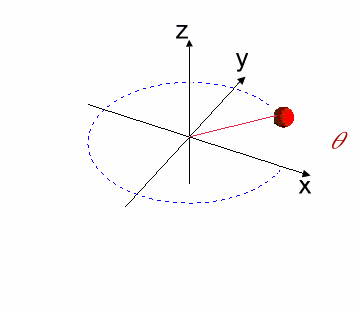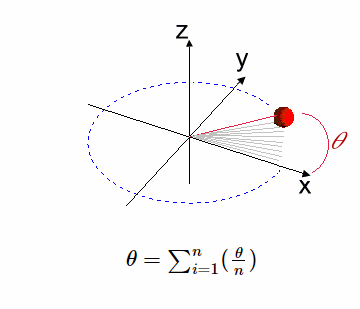
Ilustra un Rotación Infinitesimal
Así mismo si $\theta \longrightarrow 0$ entonces los valores de $cos(\theta)\longrightarrow 1$ y $sin(\theta)\longrightarrow 0$, cuyos elementos conforman $R(\theta)$.
Sea $ \epsilon=\lim\limits_{n\to\infty}(\frac{\theta}{n})$, esto significa que la matriz de rotación $R(\epsilon)\longrightarrow (I+A)$. Es decir, existe una matriz $A$ infinitesimal del mismo orden que completa la igualdad en el límite. Este supuesto de aproximación es fundamental101 para la transformación en potencias de $n\in N$ la rotación infinitesimal.
De modo que la matriz $R$ tiende a la matriz Idéntica más una matriz Infinitesimal del mismo orden.
De donde: $$ \begin{pmatrix} \epsilon_{11} & \epsilon_{12} \\ \epsilon_{21} & \epsilon_{22} \\ \end{pmatrix}+\begin{pmatrix} \epsilon_{11} & \epsilon_{21} \\ \epsilon_{12} & \epsilon_{22} \\ \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \\ \end{pmatrix} $$ Operando:
Por tanto, la matriz $A$, - obtenida bajo las características de Grupo de Lie $[L1.2]$ -, es Antisimétrica, dado que $(A + A^{T})= 0$ es su definición. Si aplicamos, la definición sobre una matriz real de $2\times 2$ entonces se obtiene una matriz de la forma siguiente:
A continuación, veremos la recursividad de las derivadas de $[R(\theta)]^n=(I+(\frac{\theta}{n})J)^n$, a fin de aplicar la Serie de Taylor, que se expresa con la siguiente formulación en serie de potencias:
Recordar que la Serie de Taylor de una función real o compleja $f(x)$ es infinitamente diferenciable en el entorno de un número real o complejo, -en este caso-, se evalúa en $\theta=0$. La expresión $f^{\small{(n)}}$ denota la n-ésima derivada de la función evaluada $\theta$. Nótese que cuando la Serie de Taylor se evalua en $\theta=0$, la serie es también denominada: Serie de Maclaurin.
$$
\frac{dR}{d\theta}=R^{'}(\theta)=\\n(I+(\frac{\theta}{n})J)^{n-1}(\frac{J}{n})=\\(I+(\frac{\theta}{n})J)^{n-1})J\\\Rightarrow\mathbf{ R^{'}(0)=I·J = J}
$$
Calculemos entonces la enésima derivada de la serie: $$ \frac{d^{\mathit (n)}R}{d\theta}=\\R^{\mathit (n)}(\theta)=n(n-1)(n-2)(n-3)\\(I+(\frac{\theta}{n})J)^{n-4}\dots (\frac{J}{n})^n \\\Rightarrow \mathbf{R^{\mathit (n)}(0)=\\\underbrace {\require{cancel}\cancelto{}{n}(n-1)(n-2))(n-3)\\(n-4) \dots} \frac{J^n}{n^{n-1}}} $$
Luego al operar el polinomio en $n$ de la enésima derivada $R^{\mathit (n)}(0)$, se obtiene que el coeficiente principal igual a $1$ del numerador del término $n^{n-1}$, es igual que el coeficiente principal polinomio del denominador que es también $1$. Eso implica que el límite al infinito es $1$, dado que ambos polinomios tienen el mismo grado. Entonces,
Aplicando el desarrollo de polinomio con Serie de Taylor,- en torno al origen $0$ del intervalo $-\pi \le \theta \le \pi$-, a la función de rotación Infinitesimal $R(\theta)$, se obtiene lo siguiente:
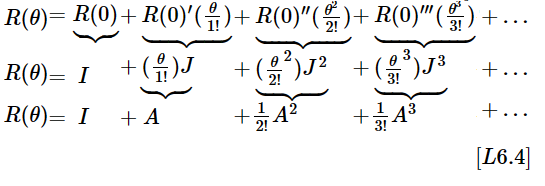
En efecto, en el polinomio se reemplaza cada término $\theta^{k}J^{k}$ por $A^{k}$ con $k=1,2,3,4, \dots$. Ver $[L6.3]$
La serie rotulada con $[L6.4]$ demuestra ser claramente la serie de Taylor para la función $\large {e^{A}}$, lo que demuestra que
$$ \large{e}^A=I + A + \frac{1}{2}A^2 + \frac{1}{3!}A^3+\frac{1}{4!}A^4 + \frac{1}{5!}A^5 + \frac{1}{6!}A^6+\frac{1}{7!}A^7+ \cdots\cdots = \sum_{k=0}^{\infty} \frac{1}{k!}A^k $$ A continuación de este desarrollo "Infinitesimal de las Rotaciones Pasivas", base del siguiente capítulo II. Enfoque Exponencial $\large{e}^A$, del Grupo de Lie de matrices $2\times 2$. |
|
II.-Enfoque Matriz Exponencial
La definición del exponencial elevado a potencias de una matriz $A$, utilizando las operaciones binarias ordinarias es semejante a las series definidas sobre el campo de los reales o complejos. Sólo que el neutro multiplicativo $1$, matricialmente es la matriz idéntica $I$.
$$ \large{e}^A=I+ A + \frac{1}{2}A^2 + \frac{1}{3!}A^3+\frac{1}{4!}A^4 +\\ \frac{1}{5!}A^5 + \frac{1}{6!}A^6+\frac{1}{7!}A^7+ \cdots\cdots =\\ \sum_{k=0}^{\infty} \frac{1}{k!}A^k \qquad\quad [L7] $$ Ahora, retomemos la matriz real $[L1]$ de rotación Especial Ortogonal de Dimensión $2$, $M_{2x2}\in SO(2)$:
Con esta matriz $A$ se va a generar un desarrollo recursivo que se expresará en potencias $A^n$.
Entonces la generación recursiva de las potencias enteras de $A$ se expresará en función de los valores de {$I, \alpha$ $J$}, con $n\in N$:
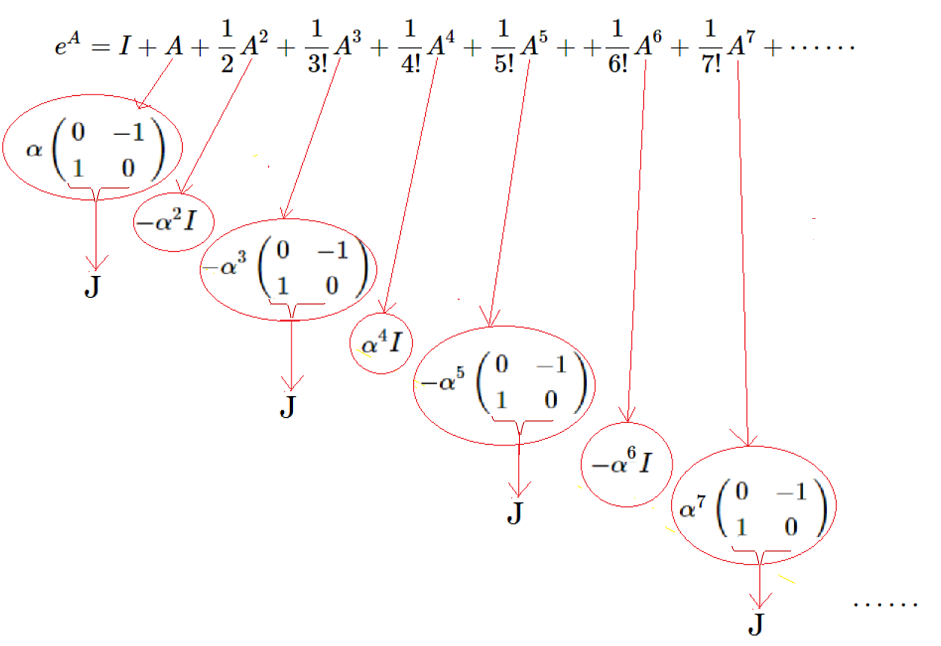 Detalle para la Sustitución {$I, \alpha$ $J$}
De modo que podemos expresar la serie $[L7]$ con el exponencial elevado a potencias de una matriz $A$, sustituyendo las matrices $I$ y $J$ en dicha serie, para obtener la siguiente expresión:
Luego, al reordenar los términos de la serie $[L8]$, separando los coeficientes enteros pares factorizados por $I$ más los coeficientes impares factorizando por $J$, se obtienen las series del coseno $[L1.2]$ y la serie del seno $[L1.1]$, en la siguiente expresión:
|
| $$\large{e}^A=$$ | $$\underbrace{(1 - \frac{1}{2}\alpha^{2} + \frac{1}{4!}\alpha^{4} + -\frac{1}{6!}\alpha^{6}+\cdots)I} $$ | + | $$\underbrace{(\frac{1}{1!}\alpha^1 - \frac{1}{3!}\alpha{^3} + \frac{1}{5!}\alpha^{5}-\frac{1}{7!}\alpha^{7} + \cdots)J}$$ |
| $$cos(\alpha)·I$$ | + | $$sin(\alpha)·J$$ |
|
$$\Rightarrow$$ $$M= cos(\alpha)\begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix} + sin(\alpha)\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix} =\begin{pmatrix} cos(\alpha) & -sin(\alpha) \\ sin(\alpha) & cos(\alpha) \\ \end{pmatrix} =\large{e}^A $$
Por tanto, hemos demostrado $M_{2x2}$ constituye el Grupo de Lie $(G,·)$ y que ambos enfoques, tanto el geométrico en el plano aplicando simple trigonometría como el enfoque Matriz Exponencial son herramientas para obtener la matriz simétrica de rotación $M_{2x2}\in SO(2)$.
|
| $$ G=\unicode{123}M\in SO(2)/Det(M)=1\land M^{T}=M^{-1}\unicode{125} $$ |
Fin del artículo junio 2021 ~ Versión Actualizada 01/09/2021 con Transición Enfoque Infinitesimal

|
Canal de Videos |
|
Notas Complementarias Adjuntas
 Cubo de Rubik Ejemplo de Grupo Simétrico de Permutación |