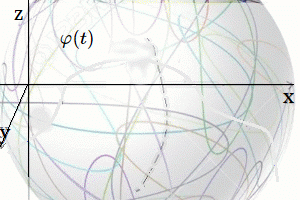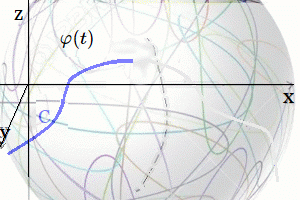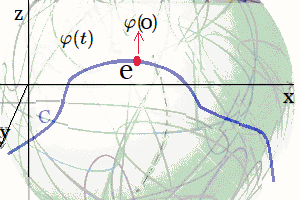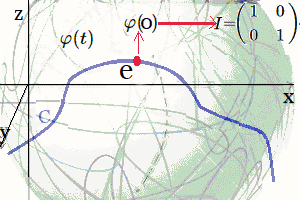|
Ecuación Diferencial
José Enrique González Cornejo
|
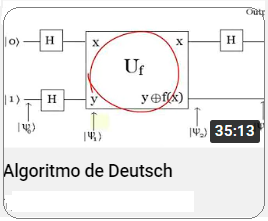
 Video Ecuación Diferencial Grupo Lineal Especial Sl2
.
Video Ecuación Diferencial Grupo Lineal Especial Sl2
.
|
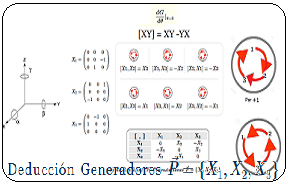
Introducción El artículo aborda el desarrollo de una ecuación diferencial asociada a las matrices generadoras del álgebra de Lie del Grupo Lineal Especial $Sl_2$. En particular, se presenta la ecuación diferencial y se explica cómo esta surge de las condiciones y propiedades del Grupo $Sl_2$. Se hacen referencias bibliográficas a publicaciones previas que tratan los conceptos necesarios para entender las transformaciones infinitesimales y las relaciones entre el grupo y su álgebra de Lie. Luego, se proporciona un ejemplo concreto de una ecuación diferencial y se muestra paso a paso cómo se resuelve. La solución de la ecuación diferencial está relacionada con una función continua y diferenciable que describe una rotación en el plano bidimensional. Se utiliza una aproximación geométrica para obtener la solución y se explican los conceptos de grupo de rotación $Sl_2$ y álgebra de Lie asociados a esta solución. Finalmente, se concluye que la solución de la ecuación diferencial representa un lugar geométrico en el plano o en una superficie suave, dependiendo del contexto, y se menciona la importancia de entender que no todas las ecuaciones diferenciales tienen soluciones explícitas en términos de funciones elementales. Se adiciona un problema resuelto $Sl_2$ con un sistema de ecuaciones. Enunciado Se muestra específicamente el desarrollo de una ecuación diferencial que proviene de las matrices generadoras del Algebra de Lie del Grupo Lineal Especial $Sl_2$1. $$ \varphi'(t) = \begin{pmatrix} -\sin(t) & -\cos(t) \\ \cos(t) & -\sin(t) \end{pmatrix}\qquad\quad \bbox[#FFFFE0]{[EC1]} $$ Es decir, $$ \large{\varphi'(t)\quad\implies \quad \varphi(t)} $$ Bajo las condiciones de existencia, de borde y de región que debe cumplir una ecuación diferencial están en el Grupo Lineal Especial $Sl_2$2. Se recuerda tener presente la definición de $Sl_2$: 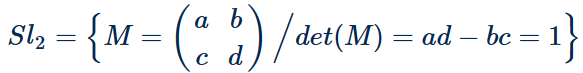
Grupo Lineal Especial en $\mathbb R$3 En las referencias bibliográficas (artículos y videos), se trataron determinados conceptos detalladamente. Conceptos que la teoría de grupos y álgebras de Lie permiten un estudio de estas transformaciones infinitesimales. Particularmente en el artículo y video de base Ejemplo Sl2 ~ Grupo Lineal Especial y sus Generadores del Algebra de Lie  . .
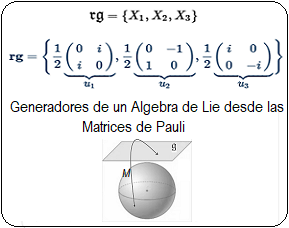
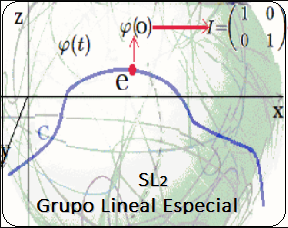
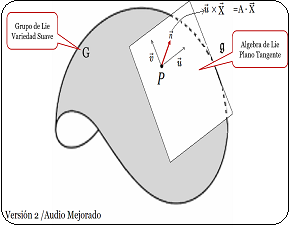
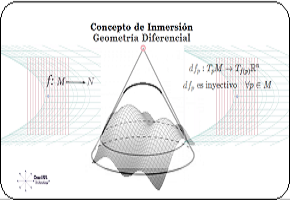
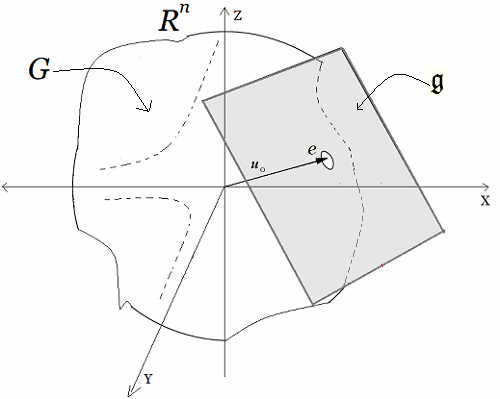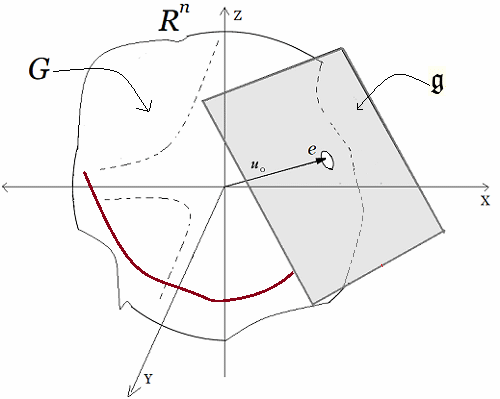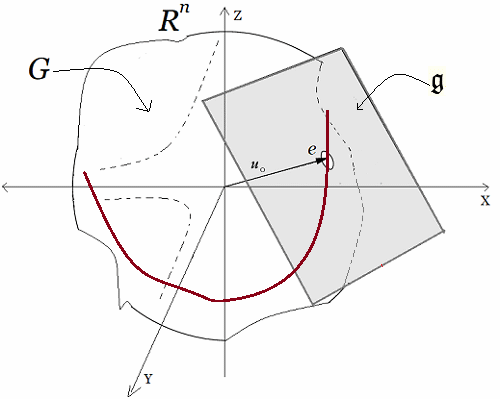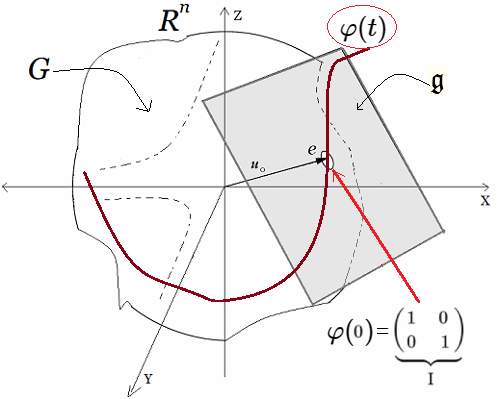
En estas publicaciones, se mostró una curva continua y diferenciable $\varphi(t)$ del grupo $Sl_2$ relacionada con su álgebra de Lie. Donde la derivada de la curva en un punto específico proporciona la base para obtener las matrices generadoras del álgebra de Lie. En otros términos, se asumió una función genérica $\varphi(t)$ que se desliza sobre una superficie suave $Sl_2$, la cual se deriva en un punto evaluado en $t=0$. Desde ahí se obtiene el plano tangente ${\large{\mathfrak {g}}}$, donde toda matriz en ese plano puede ser expresado como una combinación lineal de los generadores de base $\large{\mathfrak{rg}}=\unicode{123}E,F,H\unicode{125}\equiv \unicode{123}g_1,g_2,g_3\unicode{125}$ del álgebra de Lie $\large{\mathfrak sl(2)}$4. $$ \large{\mathfrak {rg}}= \Bigg\{ \overbrace{ \underbrace{\begin{pmatrix} 0 & 1\\ 0 & 0\\ \end{pmatrix}}_{\large{\text{E}}} }^{\large{g_1}} , \overbrace{\underbrace{\begin{pmatrix} 0 & 0\\ 1 & 0\\ \end{pmatrix}}_{\large{\text{F}}}}^{\large{g_2}}, \overbrace{ \underbrace{\begin{pmatrix} 1 & 0\\ 0 & -1\\ \end{pmatrix}}_{\large{\text{H}}}}^{\large{g_3}} \Bigg\} $$ Este concepto de representación6, constituye una herramienta fundamental en la Teoría de Lie y cuenta con aplicaciones en las más diversas áreas de la matemática y la física. Ejemplo Ecuación Diferencial Se realiza con un ejercicio predeterminado, explicando simples pasos de resolución de ecuaciones diferenciales de primer orden7 del tipo requerido para el problema en cuestión. Posteriormente se desarrollará la solución algebraica y geométrica que proviene del grupo lineal especial $Sl_2$, con sus matrices generadoras del álgebra de Lie asociadas: Sea $\varphi'(t)$, la ecuación diferencial siguiente: $$ \varphi'(t) = \begin{pmatrix} -\sin(t) & -\cos(t) \\ \cos(t) & -\sin(t) \end{pmatrix}\qquad\quad \bbox[#FFFFE0]{[EC1]} $$ La solución de $[EC1]$ es un grupo que representa una variedad diferenciable que contiene la función genérica $\varphi(t)$ sobre su superficie suave. Esta función $\varphi(t)$ es la primitiva, que dio origen a la ecuación y permite la obtención de sus matrices generadores de un álgebra de Lie, desde su plano tangente sobre un punto. (Específicamente desde el punto neutro de la función $\varphi(0)$) Nótese que desde esta conformación de grupo $Sl_2 \in GL(\mathbb R^2,\text{·})$8, se define como el conjunto de matrices de $2×2$, cuyas determinantes son igual a uno, este grupo de Lie $Sl_2$, se le asocia un Algebra de Lie $\large{\mathfrak g}$  , mediante una aproximación geométrica. , mediante una aproximación geométrica.Geométricamente, la primitiva o solución general $\varphi(t)$ , es una ecuación de una familia de curvas y una solución particular de una de las curvas integrales de la ecuación. El desarrollo de un ejemplo de resolución de la ecuación diferencial simple de primer orden $\varphi'(t) \in Sl_2(\mathbb R)$, que es la derivada de una función continua y diferenciable. 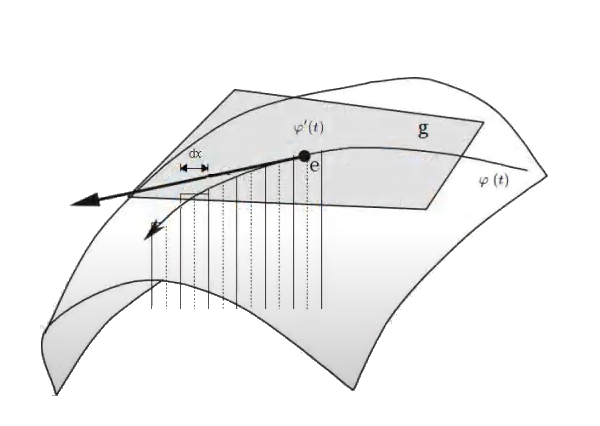  Superficie Suave o Variedad Diferencial Superficie Suave o Variedad Diferencial
En efecto, la ecuación diferencial simple que proviene del concepto de un plano tangente a una función continua y diferenciable $\varphi(t)$, que se desplaza por una superficie suave o lisa (variedad diferenciable o "manifold", que es superficie suave tridimensional, como se ilustra en la siguiente figura.). | ||||||||||||||||||||||
|
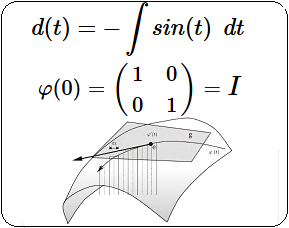
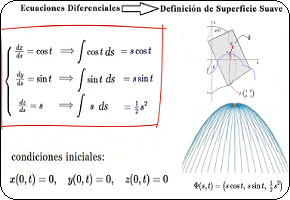
Resolución $\varphi'(t)$ [EC1] Para resolver la ecuación diferencial dada, donde la derivada de la matriz $\varphi'(t)$ está especificada, seguiremos un proceso paso a paso de la solución para resolver esta ecuación diferencial matricial que tenemos rotulada como $[EC1]$: $$ \varphi'(t) = \begin{pmatrix} -\sin(t) & -\cos(t) \\ \cos(t) & -\sin(t) \end{pmatrix} $$ El objetivo es determinar $\varphi(t)$, tal que su derivada sea igual a la matriz dada. La ecuación diferencial también se expresa como: $$ \frac{d\varphi(t)}{dt} = \begin{pmatrix} -\sin(t) & -\cos(t) \\ \cos(t) & -\sin(t) \end{pmatrix} $$ 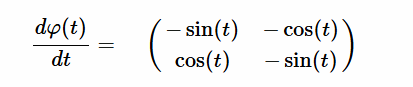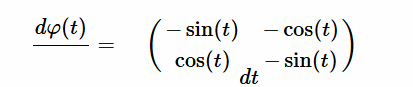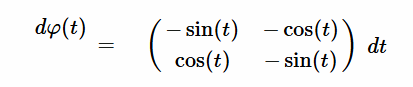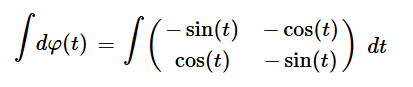 Es decir, las entradas de $\varphi'(t)$ son funciones lineales de una variable $t$. Donde la derivada de la matriz $\varphi'(t)$, es la igual a la matriz de cada uno de sus elementos derivados: $$ \varphi'(t) = \begin{pmatrix} a'(t) & b'(t) \\ c'(t) & d'(t) \end{pmatrix} = \begin{pmatrix} -\sin(t) & -\cos(t) \\ \cos(t) & -\sin(t) \end{pmatrix} $$ Así mismo, la integral de $\varphi'$ con respecto a $t$, definida en un intervalo cerrado real $[a,b]$ se denota como $\int \varphi'(t) \phantom{2}dt$ y se expresa como: $$ \int \varphi'(t)\phantom{2}dt = \begin{pmatrix} \int a'(t)\phantom{2}dt & \int b'(t)\phantom{2}dt\\ \int c'(t)\phantom{2}dt & \int d'(t)\phantom{2}dt \end{pmatrix} $$ Se iguala la derivada $\varphi'(t)$ con la matriz dada $[EC1]$: $$ \begin{pmatrix} a'(t) & b'(t) \\ c'(t) & d'(t) \end{pmatrix} = \begin{pmatrix} -\sin(t) & -\cos(t) \\ \cos(t) & -\sin(t) \end{pmatrix} $$ Integando en ambos miembros, se obtiene: $$ \begin{pmatrix} \int a'(t)\phantom{2}dt& \int b'(t)\phantom{2}dt \\ \int c'(t)\phantom{2}dt & \int d'(t)\phantom{2}dt \end{pmatrix} = \begin{pmatrix} -\int \sin(t)\phantom{2}dt & -\int \cos(t)\phantom{2}dt \\ \int \cos(t)\phantom{2}dt & -\int \sin(t)\phantom{2}dt \end{pmatrix} $$ Resulta que cada elemento de la matriz $\varphi'(t)$ será una ecuación diferencial individual a integrar:
Luego, resolvemos cada una de estas ecuaciones diferenciales por separado. Integrando:
Donde $c_1,c_2,c_3,c_4$ son una constantes de integración. Para determinar estas constantes de integración, se usa las condiciones iniciales, sabiendo que $\varphi(0)=\large{I}$, i.e. la matriz identidad: $$ \varphi(0) = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}=\large{I} $$ Se evalúan las soluciones en $t = 0$:
Se igualan con los valores de la matriz idéntica, de donde $c1=c2=c3=c4=0$:
Por lo tanto, las soluciones para $a(t)$, $b(t)$, $c(t)$ y $d(t)$ son:
Entonces ensamblando los elementos en la matriz $\varphi(t)$ se obtiene la solución la ecuación diferencial $[EC1]$ : $$ \bbox[white,15px,border:1px solid #c0c0c0]{ \varphi(t) = \begin{pmatrix} \cos(t) & -\sin(t) \\ \sin(t) & \cos(t) \end{pmatrix}} $$ $$\bbox[#FFFFE0]{[EC2]}$$ Es necesario agregar que $\varphi(t)$, corresponde a un operador de rotación de $2×2$, definido en los reales y corresponde a un Grupo de Lie de rotación ortogonal especial $SO(2)$, i.e. es un operador definido en los reales, - en el espacio euclídeo -, y que es un grupo lineal especial $Sl_2$, pero además ortogonal. Nótese que $SO2 \subset Sl_2$.
Generador Simple desde la Solución $\varphi(t)$ A continuación se observa que la solución $[EC2]$ es un grupo de rotación en $\varphi(t) \in SO(2)$, de donde también se obtiene un generador $X$ simple del Algebra de Lie. En efecto, geométricamente, el generador $ X $ del grupo de rotación $ SO(2) $ representa la dirección instantánea de la rotación alrededor del origen en el plano bidimensional, y se obtiene tomando la derivada de la función $ \varphi(t) $ con respecto a $ t $, evaluada en $ t = 0 $. 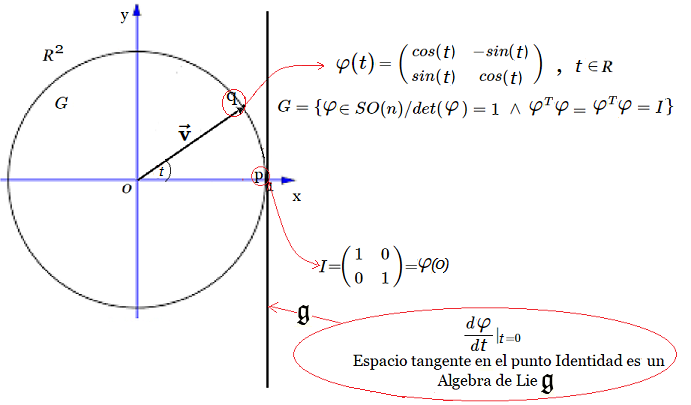 La figura muestra un círculo contenido en $\large {\mathbb {R^2}}$, con un vector longitud $\large{|\vec{v}|=1}$ y ángulo $\large{t}$, donde el punto $\large{q}$ tiene asociada la matriz $\large{\varphi_{2 \times 2}(t)}$, - que es la operador de rotación que constituye un Grupo de Lie en $SO(2)$ -, y la recta tangente en el punto $\large{p}=(1,0)$, - que corresponde al elemento Identidad -. Luego, la recta tangente es un Algebra de Lie $\large{\mathfrak {g}}$ y su generador se señala a continuación: $$X=\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}$$ Este generador antisimétrico $X \in SO(2)$, se obtiene del diferencial de la matriz $\varphi_{2 \times 2}(t)$ evaluada en $t = 0$: $$\frac{d\varphi}{dt}\mid_{t=0}$$ Efectivamente: $$ \varphi(t)=\begin{pmatrix} cos(t) & -sin(t) \\ sin(t) & cos(t) \\ \end{pmatrix}$$ $$\Rightarrow$$ $$\frac{d\varphi(t)}{dt}=\begin{pmatrix} -sin(t) & -cos(t) \\ cos(t) & -sin(t) \\ \end{pmatrix} $$ $$\Rightarrow$$ $$\frac{d\varphi(t)}{dt}\mid_{t=0}=\begin{pmatrix} -sin(0) & -cos(0) \\ cos(0) & -sin(0) \\ \end{pmatrix}=\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}=X$$ Se observa que la función $ \varphi(t) $ describe la rotación de un vector en el plano bidimensional en función del ángulo $ t $. El generador $ X $ del grupo de rotación $ SO(2) $ representa la dirección instantánea del movimiento en el origen causado por una rotación infinitesimal. Nótese que el vector unitario $ \mathbf{\vec {v}} $ en el plano bidimensional que inicialmente apunta en la dirección del eje $ x $. A medida que aplicamos la función $ \varphi(t) $, el vector $ \mathbf{\vec{v}} $ rota en algún sentido de las agujas del reloj alrededor del origen. 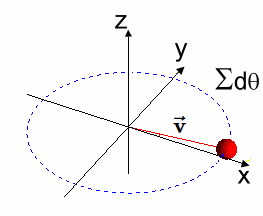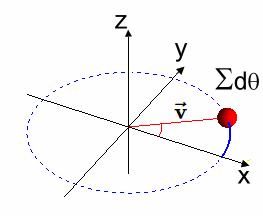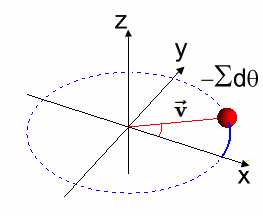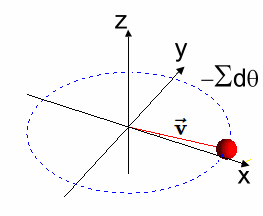
La dirección de este movimiento se puede visualizar como la dirección en la que el vector $ \mathbf{\vec {v}} $ se mueve cuando $ t $ se incrementa infinitesimalmente alrededor de $ t = 0 $. En otros términos, $ X $ es el vector tangente a la trayectoria seguida por el vector $ \mathbf{\vec {v}} $ en el origen cuando se realiza una rotación infinitesimal.  ) )Conclusión En conclusión, se dice que la matriz $\varphi(t)$ satisface la ecuación diferencial dada y representa una rotación en el plano. $$ \overbrace{ \underbrace{\begin{pmatrix} -sin(t) & cos(t)\\ -cos(t) & -sin(t)\\ \end{pmatrix}}_{\large{\text{[EC1]}}} }^{\large{\varphi'(t)}} \implies \overbrace{\underbrace{\begin{pmatrix} cos(t) & sin(t)\\ -sin(t) & cos(t)\\ \end{pmatrix}}_{\large{\text{[EC2]}}}}^{\large{\varphi(t)}} $$ |
||||||||||||||||||||||
|
Es decir la solución $\varphi(t)_{2\times 2}$ que se muestra en $[EC2]$, además de ser lineal y especial en $Sl_2$, es ortogonal, i.e. $SO(2) \subset Sl_2$.
Por lo tanto, $\varphi(t)\in G$, donde $G$ es el conjunto de todas las matrices de $\varphi_{2\times 2}$ ortogonales que pertenecen al 'Special Ortogonal of order 2' del espacio euclídeo tridimensional con determinante igual la unidad9. $$ \varphi(t) = \begin{pmatrix} \cos(t) & -\sin(t) \\ \sin(t) & \cos(t) \end{pmatrix} $$ $$ G=\unicode{123} \varphi\in SO(2)/Det(\varphi)=1 \land \varphi^{T}=\varphi^{-1}\unicode{125} $$ En otras palabras, en el presente artículo se ilustró un método para resolver la ecuación diferencial $[EC1]$, y así obtener efectivamente la solución $[EC2]$. Es necesario observar que una ecuación diferencial no necesariamente debe tener solución, y aun así (a veces) es posible encontrar una solución cuando ella existe. Aunque no siempre es una fórmula explícita, en términos de funciones elementales, que satisfagan la ecuación. En muchos casos, particularmente en el estudio de ecuaciones no lineales, puede ser que tengamos que conformarnos sólo con obtener aproximaciones de una solución. En este caso, si existe una solución de la ecuación diferencial. Entonces esa solución, representa un lugar geométrico (puntos conectados por una curva continua) sea en el plano cartesiano o en una superficie suave. |
|
Problema Resuelto
Dado el grupo de rotaciones en el plano $SO(2)\subset Sl_2$, con el siguiente sistema de ecuaciones: $$ \large{ \begin{matrix} \overline{x}=\phantom{4}x\cos(t) + y\sin(t)\\ \overline{y}=-x\sin(t) + y\cos(t) \end{matrix} } $$
|
|
Respuesta Cálculo del generador infinitesimal El generador infinitesimal de un grupo de Lie se define como la derivada en $ t $ de la matriz de rotación $ R(t) $10 evaluada en $ t = 0 $. En el caso de $SO(2)$, la matriz de rotación es: $$ R(t) = \begin{pmatrix} \cos(t) & \sin(t) \\ -\sin(t) & \cos(t) \end{pmatrix} $$ Entonces, para calcular el generador infinitesimal se deriva $ R(t) $ respecto a $ t $ y se evalúa en $ t = 0 $: $$ \begin{align*} \frac{dx'}{dt} &= -x \sin(t) + y \cos(t) \\ \frac{dy'}{dt} &= -x \cos(t) - y \sin(t) \end{align*} $$ Por lo tanto, el generador infinitesimal es: $$ \large{G = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}} $$ (Se sabe que $\sin'(t)=-\cos(t)\quad \land \quad \cos'(t)=\sin(t)$, asímismo que $\sin(0)=0,\quad \land \quad \cos(0)=1$) Esta matriz unitaria y antisimétrica es el generador infinitesimal del grupo $SO(2)$. Sumar la serie de Lie La serie de Lie se puede expresar como: $$ R(t) = \large{e}^{tG} $$ Donde $ R(t) $ es la matriz de rotación para un ángulo $ t $ y $ G $ es el generador infinitesimal del grupo. Para $SO(2)$: $$ G = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} $$ Entonces la serie de Lie se convierte en: $$ R(t) = \large{e}^{t \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}} $$ Para calcular $ \large{e}^{tG} $, se puede utilizar la expansión en series de Taylor de la función exponencial: $$ \large{e}^{tG} = \sum_{n=0}^{\infty} \frac{(tG)^n}{n!} $$ Sea $A=tG$. Entonces $\large{e}^{tG}=\large{e}^{A}$: $$ \large{e}^{A}=I + A + \frac{1}{2}A^2 + \frac{1}{3!}A^3+ \cdots = \sum_{k=0}^{\infty} \frac{1}{k!}A^k $$ $$R(t)=\large{e}^A=\large{e}^{t G}=\large{e}^{t \small{\begin{pmatrix} 0 & -1 \\1 & 0 \\ \end{pmatrix}}}$$ Integrar el problema de valor inicial El problema de valor inicial implica encontrar la solución de las ecuaciones diferenciales dadas con una condición inicial. En este caso, las ecuaciones diferenciales son las mismas que definen las rotaciones en $SO(2)$. La condición inicial podría ser $ (x_0, y_0) $, es decir, las coordenadas iniciales del punto que estamos rotando. Encontrar las coordenadas canónicas Las coordenadas canónicas generalmente se refieren a las coordenadas en las que las ecuaciones del problema se escriben de la forma más simple posible. En este caso, las coordenadas canónicas podrían ser las coordenadas polares $ (r, \theta) $, donde $ r $ es la distancia desde el origen y $ \theta $ es el ángulo de rotación. Determinar los puntos y las familias de curvas invariantes Los puntos invariantes son aquellos que no cambian bajo la acción del grupo de rotación $SO(2)$. Estos son simplemente los puntos en el plano que se encuentran en el eje de rotación. Las familias de curvas invariantes son conjuntos de curvas que no cambian de forma bajo la acción de las rotaciones. Por ejemplo, todas las líneas que pasan por el origen son familias de curvas invariantes, ya que se rotan alrededor del origen manteniendo su forma. Es decir, los puntos en la intersección de las líneas $x=0$ y $y=0$, que es el origen $(0,0)$, son invariantes bajo la acción de $SO(2)$.  |