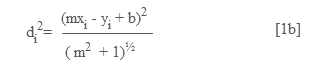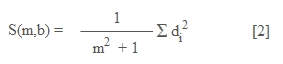Introducción

En reiteradas ocasiones remarcamos que un modelo constituye una representación abstracta y esquemática de determinados aspectos de la realidad.  La  estructura de un modelo está formada por los elementos que se relacionan, y en la mayoría de las veces se debe trabajar con Ordenes de Magnitud, en el sentido de proyectar mediciones.

En nuestro caso estamos interesados en los modelos matemáticos. Es decir, modelos formales basados en la lógica y un conjunto de relaciones matemáticas (tales como ecuaciones, inecuaciones, relaciones lógicas, probabilidades, elasticidades, cambios, regresiones, valores iniciales a priori, etc.) que intentan representar la realidad.

DocIRS conforma con el cliente un equipo multidisciplinario, para trabajar conjuntamente el modelamiento requerido. Generalmente,  se deben estimar coeficientes y distribuciones para el modelamiento, mediante:

i)                    Regresiones Lineales, utilizando el método de los mínimos cuadrados.

ii)                  Teorema de Bayes

iii)                Cadenas de Marcov

iv)        Funciones de Distribución Estadística

A este fin, DocIRS no sólo está apoyando al tratamiento sobre bases de datos, modelamiento computacional, sino también a solventar y recordar una serie de conceptos tales como las  Transformaciones (logarítmicas u otras), isocuantas (Cobb -Douglas), Matrices,  Probabilidades , Distribuciones Estadísticas, etc.. y formas simples de utilización de funciones y complementos del Excel para los cálculos e estimaciones

Desarrollaremos un número determinado de ejemplos orientados a la comprensión, comenzaremos con un ejemplo simple de una función lineal en una sola variable para ir introduciendo la utilización de métodos lineales y estimación de mínimos cuadrados en varias variables:

Mínimos Cuadrados

En el presente capítulo explicaremos el método de optimización o búsqueda del mínimo, con un ejemplo de sólo tres observaciones, a fin explicar en forma simple el método con que se obtienen los coeficientes de la curva que mejor aproxima. Obviamente, cuando se trabaja en tratamiento estadístico de datos el tamaño de las muestras es considerablemente mayor. (Ver Regresión Múltiple)

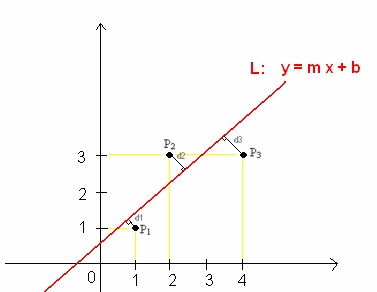
Supongamos tenemos tres observaciones en el plano cartesiano. Es decir, tres pares ordenados de datos en los Reales (R²) :

P₁: (1,1)

P₂: (2,3)

P₃: (4,3)

Deseamos buscar la recta L, que aproxime las observaciones cumpliendo con la condición de los mínimos cuadrados. Es decir, minimizando la sumatoria de las distancias al cuadrado, de los puntos dados a dicha recta.

A ese efecto, construiremos una función S de varias de variables, la cual contenga la sumatoria de las desviaciones al cuadrado, que optimizaremos,  derivándola parcialmente e igualando a cero para encontrar el mínimo.

Una vez determinada la función, mediante cálculos realizados manualmente, estimaremos los coeficientes también mediante regresiones con Excel.

Donde d₁, d₂ y d₃ son las distancias más cortas de los puntos P₁, P₂ y P₃ respectivamente a las recta L que deseamos determinar.

Sabemos que la distancia d_i de un punto dado (x_{i ,} y_i) a una recta dada  y = mx + b se calcula con la siguiente formula (que demostraremos más adelante):

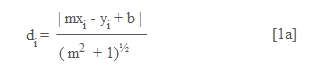
(Ver demostración en Distancia de un Punto a una Recta)

=>

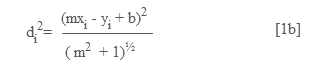
Donde m es la pendiente y b el intercepto de la recta y

Sea S(m,b)  una función cuyas variables son la pendiente m y el intercepto de la recta b,  que representa la suma de los cuadrados de las distancias, de modo que:

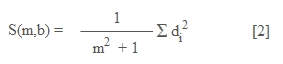
Nota: La constante 1/ (m²  + 1) la obviaremos de la función, dado que no aporta en el estudio de la variación que realizaremos en la optimización de la función [2].

Luego, utilizando las expresiones [1b] y [2], con ejemplo con los puntos dados P₁, P₂ y P₃  , la función a optimizar adquiere la siguiente forma:

S(m,b)  = (m - 1+ b) ² + (2m - 3 + b) ² + (4m - 3 + b) ²

Derivando parcialmente la función S(m,b):

Con respecto a m se obtiene:

=>

Con respecto a b se obtiene:

=>

Por tanto igualando a cero las derivadas [i] y [ii]  se obtiene el siguiente sistema de ecuaciones:

21 m + 7 b =   14

7 m + 3 b =  7

Resolviendo el sistema de ecuaciones se tiene:

m =  4/7

b =  1

=>  Que el punto Q = (4/7, 1) minimiza la función S(m,b)

Por tanto la recta L es:

y = 4/7 x + 1

Es decir, L es la función lineal que cumple las condiciones de lo mínimos cuadrados, para los puntos dados en el plano cartesiano.

Nótese que Q es un punto crítico de S, puesto que las derivadas parciales de primer orden de S están definidas en todos los puntos de una región del plano xy, y Q es el extremo relativo de S en la región donde están situados en puntos críticos.

Solución Directa con Excel

Mostraremos la solución utilizando el complemento Herramientas para Análisis de Excel, a partir del cual podemos resolver vía regresión lineal muestras de observaciones de mayor orden y en varias variables. Nótese que la herramienta no sólo calcula el intercepto (b=1) y coeficientes (m= 4/7 = 0,57142857), sino que una serie de otros estimadores asociados a las sumas de las desviaciones y errores al cuadrado.